Barometric formula

For broader coverage of this topic, see Vertical pressure variation.

The barometric formula is a formula used to model how the air pressure (or air density) changes with altitude.

Model equations

See also: Atmospheric pressure

Pressure as a function of the height above the sea level

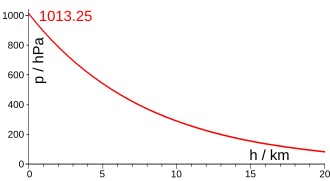
The U.S. Standard Atmosphere gives two equations for computing pressure as a function of height, valid from sea level to 86 km altitude. The first equation is applicable to the atmospheric layers in which the temperature is assumed to vary with altitude at a non null temperature gradient of $L_{M,b}$: $$P=P_{b}\cdot \left[{\frac {T_{M,b}}{T_{M,b}+L_{M,b}\cdot \left(H-H_{b}\right)}}\right]^{\frac {g_{0}'\cdot M_{0}}{R^{*}\cdot L_{M,b}}}$$ .

The second equation is applicable to the atmospheric layers in which the temperature is assumed not to vary with altitude (zero temperature gradient): $$P=P_{b}\cdot \exp \left[{\frac {-g_{0}'\cdot M_{0}\left(H-H_{b}\right)}{R^{*}\cdot T_{M,b}}}\right]$$ , where:

• $P_{b}$ = reference pressure
• $T_{M,b}$ = reference temperature (K)
• $L_{M,b}$ = temperature gradient (K/m), e.g. -6.5 K/km at sea level. This is the lapse rate with the opposite sign convention.
• $H$ = geopotential height at which pressure is calculated (m)
• $H_{b}$ = geopotential height of reference level b (meters; e.g., H_b = 11 000 m)
• $R^{*}$ = universal gas constant: 8.31432 N·m/(kmol·K)
• $g_{0}'$ = The gravitational acceleration in units of geopotential height, 9.80665 m/s²
• $M_{0}$ = mean molecular weight of air at sea level: 28.9644 kg/kmol

Or converted to imperial units:

• $P_{b}$ = reference pressure
• $T_{M,b}$ = reference temperature (K)
• $L_{M,b}$ = temperature gradient (K/ft)
• $H$ = height at which pressure is calculated (ft)
• $H_{b}$ = height of reference level b (feet; e.g., H_b = 36,089 ft)
• $R^{*}$ = universal gas constant; using feet, kelvins, and (SI) moles: 8.9494596×10⁴ lb·ft²/(lb-mol·K·s²)
• $g_{0}$ = gravitational acceleration: 32.17405 ft/s²
• $M$ = molar mass of Earth's air: 28.9644 lb/lb-mol

The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. In these equations, g₀, M and R^* are each single-valued constants, while P, L, T, and H are multivalued constants in accordance with the table below. The values used for M, g₀, and R^* are in accordance with the U.S. Standard Atmosphere, 1976, and the value for R^* in particular does not agree with standard values for this constant. The reference value for P_b for b = 0 is the defined sea level value, P₀ = 101 325 Pa or 29.92126 inHg. Values of P_b of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when H = H_b+1.

Subscript b	Geopotential height above MSL (H)		Static pressure		Standard temperature (K)	Temperature gradient		Exponent g0 M / R L
	(km)	(ft)	(Pa)	(inHg)		(K/km)	(K/ft)
0	0	0	101 325	29.9213	288.15	-6.5	-0.0019812	-5.25588
1	11	36 089	22 632.1	6.68324	216.65	0.0	0.0	—
2	20	65 617	5 474.89	1.616734	216.65	1.0	0.0003048	34.1626
3	32	104 987	868.019	0.256326	228.65	2.8	0.00085344	12.2009
4	47	154 199	110.9063	0.0327506	270.65	0.0	0.0	—
5	51	167 323	66.9389	0.0197670	270.65	-2.8	-0.00085344	-12.2009
6	71	232 940	3.95642	0.00116833	214.65	-2	-0.0006096	-17.0813

Density can be calculated from pressure and temperature using

$\rho ={\frac {P\cdot M_{0}}{R^{*}\cdot T_{M}}}={\frac {P\cdot M}{R^{*}\cdot T}}$ , where

• $M_{0}$ is the molecular weight at sea level
• $M$ is the mean molecular weight at the altitude of interest
• $T$ is the temperature at the altitude of interest
• $T_{M}=T\cdot {\frac {M_{0}}{M}}$ is the molecular-scale temperature.

The atmosphere is assumed to be fully mixed up to about 80 km, so $M=M_{0}$ within the region of validity of the equations presented here.

Alternatively, density equations can be derived in the same form as those for pressure, using reference densities instead of reference pressures.

This model, with its simple linearly segmented temperature profile, does not closely agree with the physically observed atmosphere at altitudes below 20 km. From 51 km to 81 km it is closer to observed conditions.

Derivation

The barometric formula can be derived using the ideal gas law: $$P={\frac {\rho }{M}}{R^{*}}T$$

Assuming that all pressure is hydrostatic: $$dP=-\rho g\,dz$$ and dividing this equation by $P$ we get: $${\frac {dP}{P}}=-{\frac {Mg\,dz}{R^{*}T}}$$

Integrating this expression from the surface to the altitude z we get: $$P=P_{0}e^{-\int _{0}^{z}{Mgdz/R^{*}T}}$$

Assuming linear temperature change $T=T_{0}-Lz$ and constant molar mass and gravitational acceleration, we get the first barometric formula: $$P=P_{0}\cdot \left[{\frac {T}{T_{0}}}\right]^{\textstyle {\frac {Mg}{R^{*}L}}}$$

Instead, assuming constant temperature, integrating gives the second barometric formula: $$P=P_{0}e^{-Mgz/R^{*}T}$$

In this formulation, R^* is the gas constant, and the term R^*T/Mg gives the scale height (approximately equal to 8.4 km for the troposphere).

The derivation shown above uses a method that relies on classical mechanics. There are several alterantive derivations, the most notable are the ones based on thermodynamic forces and statistical mechanics.

(For exact results, it should be remembered that atmospheres containing water do not behave as an ideal gas. See real gas or perfect gas or gas for further understanding.)

See also

• Hypsometric equation
• NRLMSISE-00