D6 polytope
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (February 2023) |
 6-demicube |
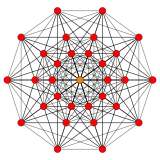
 6-orthoplex |
In 6-dimensional geometry, there are 47 uniform polytopes with D6 symmetry, of which 16 are unique and 31 are shared with the B6 symmetry. There are two regular forms, the 6-orthoplex, and 6-demicube with 12 and 32 vertices respectively.
They can be visualized as symmetric orthographic projections in Coxeter planes of the D6 Coxeter group, and other subgroups.
Graphs
[edit]Symmetric orthographic projections of these 16 polytopes can be made in the D6, D5, D4, D3, A5, A3, Coxeter planes. Ak has [k+1] symmetry, Dk has [2(k-1)] symmetry. B6 is also included although only half of its [12] symmetry exists in these polytopes.
These 16 polytopes are each shown in these 7 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.
| # | Coxeter plane graphs | Coxeter diagram Names | ||||||
|---|---|---|---|---|---|---|---|---|
| B6 [12/2] |
D6 [10] |
D5 [8] |
D4 [6] |
D3 [4] |
A5 [6] |
A3 [4] | ||
| 1 |  |
 |
 |
 |
 |
 |
 |
6-demicube Hemihexeract (hax) |
| 2 |  |
 |
 |
 |
 |
 |
 |
cantic 6-cube Truncated hemihexeract (thax) |
| 3 |  |
 |
 |
 |
 |
 |
 |
runcic 6-cube Small rhombated hemihexeract (sirhax) |
| 4 |  |
 |
 |
 |
 |
 |
 |
steric 6-cube Small prismated hemihexeract (sophax) |
| 5 |  |
 |
 |
 |
 |
 |
 |
pentic 6-cube Small cellated demihexeract (sochax) |
| 6 |  |
 |
 |
 |
 |
 |
 |
runcicantic 6-cube Great rhombated hemihexeract (girhax) |
| 7 |  |
 |
 |
 |
 |
 |
 |
stericantic 6-cube Prismatotruncated hemihexeract (pithax) |
| 8 |  |
 |
 |
 |
 |
 |
 |
steriruncic 6-cube Prismatorhombated hemihexeract (prohax) |
| 9 |  |
 |
 |
 |
 |
 |
 |
Stericantic 6-cube Cellitruncated hemihexeract (cathix) |
| 10 |  |
 |
 |
 |
 |
 |
 |
Pentiruncic 6-cube Cellirhombated hemihexeract (crohax) |
| 11 |  |
 |
 |
 |
 |
 |
 |
Pentisteric 6-cube Celliprismated hemihexeract (cophix) |
| 12 |  |
 |
 |
 |
 |
 |
 |
Steriruncicantic 6-cube Great prismated hemihexeract (gophax) |
| 13 |  |
 |
 |
 |
 |
 |
 |
Pentiruncicantic 6-cube Celligreatorhombated hemihexeract (cagrohax) |
| 14 |  |
 |
 |
 |
 |
 |
 |
Pentistericantic 6-cube Celliprismatotruncated hemihexeract (capthix) |
| 15 |  |
 |
 |
 |
 |
 |
 |
Pentisteriruncic 6-cube Celliprismatorhombated hemihexeract (caprohax) |
| 16 |  |
 |
 |
 |
 |
 |
 |
Pentisteriruncicantic 6-cube Great cellated hemihexeract (gochax) |
References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. "6D uniform polytopes (polypeta)".
