Draft:History of number theory
 | Draft article not currently submitted for review.
This is a draft Articles for creation (AfC) submission. It is not currently pending review. While there are no deadlines, abandoned drafts may be deleted after six months. To edit the draft click on the "Edit" tab at the top of the window. To be accepted, a draft should:
It is strongly discouraged to write about yourself, your business or employer. If you do so, you must declare it. Where to get help
How to improve a draft
You can also browse Wikipedia:Featured articles and Wikipedia:Good articles to find examples of Wikipedia's best writing on topics similar to your proposed article. Improving your odds of a speedy review To improve your odds of a faster review, tag your draft with relevant WikiProject tags using the button below. This will let reviewers know a new draft has been submitted in their area of interest. For instance, if you wrote about a female astronomer, you would want to add the Biography, Astronomy, and Women scientists tags. Editor resources
Last edited by Toukouyori Mimoto (talk | contribs) 25 hours ago. (Update) |
originally forked from the history section in the number theory article

Number theory is one of the oldest branches of mathematics alongside geometry. It arose out of problems related to multiplications and division of integers. Prehistoric humans performed rudimentary arithmetic with tally marks as early as 43,000 years ago. Ancient civilisations developed a more complex approach to numbers. The ancient Greeks developed a keen interest in divisibility. The Pythagoreans attributed mystical quality to perfect and amicable numbers. Parts of Euclid's Elements (3rd century BC) studied number theory, employing formal proofs and transitioning away from numerology. Diophantus (3rd century) made contributions to equations where integer solutions are of interest. After the fall of Rome, development shifted to Asia, albeit intermittently. Chinese authors studied number theory for astronomy and the calendar, with their work culminating in the Chinese remainder theorem. In India, Brahmagupta (7th century AD) innovated the use of zero and negative numbers and studied Pell's equations. Prior to the Renaissance, the development of number theory was overshadowed by other fields, such as algebra in the Islamic Golden Age.
Number theory witnessed a resurgence in Europe following the contributions of Pierre de Fermat (1601-1665), albeit it was again overshadowed by the development of calculus. He famously conjectured what would become Fermat's Last Theorem, and studied prime numbers. Leonhard Euler (1707-1783) authored over one thousand pages about number theory, frequently solving Fermat's assertions and extending ancient Greek works. Three European contemporaries continued the work in elementary number theory: Joseph-Louis Lagrange proved the four-square theorem and Wilson's theorem, Adrien-Marie Legendre proved specific cases of Fermat's Last Theorem, and Carl Friedrich Gauss introduced congruences.
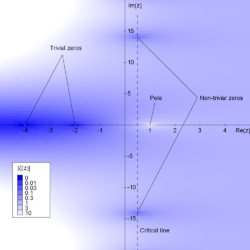
Euler's study of the zeta function formed a basis for the subfield of analytic number theory. Peter Gustav Lejeune Dirichlet (1805-1859) pioneered the subfield's methods with a proof of his analytic theorem on arithmetic progressions. The subfield studies the distribution of primes and seeks for a function that approximates it. For example, would be proved by the end of the 19th century. Bernhard Riemann (1826-1866) found a connection between the zeta function and the prime-counting function, which he conjectured to be valid. By the 20th century, a plethora of subfields had had emerged, including algebraic, geometric, and combinatorial number theory. Algebraic number theory closed the millennium with the proof of Fermat's Last Theorem by Andrew Wiles.
Open questions remain, such as the Riemann hypothesis that is among the seven Millennium Prize Problems, Goldbach's conjecture on the representation of even numbers as the sum of two primes, and the existence of odd perfect numbers. Number theory was once regarded as the canonical example of pure mathematics with no applications outside the field. In 1970s, it became known that prime numbers would be used as the basis for the creation of public-key cryptography algorithms. Schemes such as RSA are based on the difficulty of factoring large composite numbers into their prime factors. Elementary number theory is taught in discrete mathematics courses for computer scientists.
Conception
[edit]
Number theory is the branch of mathematics that studies the structure and properties of integers as well as the relations and laws between them.[1] The integers comprise a set that extends the set of natural numbers to include their negations and the number .[2]
Number theory is closely related to arithmetic and some authors use the terms as synonyms.[3] However, the word "arithmetic" is used today to mean the study of numerical operations and extends to the real numbers.[4] In a more specific sense, number theory is restricted to the study of integers and focuses on their properties and relationships such as divisibility, factorization, and primality.[5] Traditionally, it is known as higher arithmetic.[6]
By the early twentieth century, the term number theory or theory of numbers had been widely adopted.[note 1] The term number refers either to natural numbers or whole numbers, the latter of which means either the positive integers or all integers.[7][8][9] There is no consensus on the precise definition of number theory as to whether it is construed to the integers or natural numbers.[10][11] The wider scope of the integers is more convenient most purposes.[12]
The earliest forms of arithmetic are sometimes traced back to counting and tally marks used to keep track of quantities. Some historians suggest that the Lebombo bone (dated about 43,000 years ago) and the Ishango bone (dated about 22,000 to 30,000 years ago) are the oldest arithmetic artifacts but this interpretation is disputed.[13] The latter bone is claimed to list a sequence of prime numbers, though this is highly disputed. Opponents argue that the concepts of division and prime numbers evolved only around 10,000 BC in agricultural civilisations and 500 BC in ancient Greece, respectively.[14] However, a basic sense of numbers may predate these findings and might even have existed before the development of language.[15] Number theory arose out of problems related to multiplications and division of integers.[16]
Ancient history
[edit]Early development
[edit]Based on written evidence, knowledge of numbers existed in the ancient civilisations of Mesopotamia, Egypt, China, and India.[17] The first positional numeral system was developed by the Babylonians starting around 1800 BCE. This was a significant improvement over earlier numeral systems since it made the representation of large numbers and calculations on them more efficient.[18]

The earliest historical find of an arithmetical nature is a fragment of a Babylonian tablet. Plimpton 322, dated c. 1800 BC, contains a list of Pythagorean triples, that is, integers such that . The triples are too numerous and too large to have been obtained by brute force.[19][20] The table's layout suggests that it was constructed by means of what amounts, in modern language, to the identity
which is implicit in routine Old Babylonian exercises. If some other method was used, the triples were first constructed and then reordered by , presumably for actual use as a "table", for example, with a view to applications.[21]
It is not known what these applications may have been, or whether there could have been any; Babylonian astronomy, for example, truly came into its own many centuries later. It has been suggested instead that the table was a source of numerical examples for school problems.[22][note 2] Plimpton 322 tablet is the only surviving evidence of what today would be called number theory within Babylonian mathematics, though a kind of Babylonian algebra was much more developed.[23]
The Rhind Mathematical Papyrus, from around 1550 BC, has Egyptian fraction expansions of different forms for prime and composite numbers.[24]
Ancient Greece
[edit]However, the earliest surviving records of the study of prime numbers come from the ancient Greek mathematicians, who called them prōtos arithmòs (πρῶτος ἀριθμὸς). Euclid's Elements (c. 300 BC) proves the infinitude of primes and the fundamental theorem of arithmetic, and shows how to construct a perfect number from a Mersenne prime.[25] Another Greek invention, the Sieve of Eratosthenes, is still used to construct lists of primes.[26][27]
Although other civilizations probably influenced Greek mathematics at the beginning,[28] all evidence of such borrowings appear relatively late,[29][30] and it is likely that Greek arithmētikḗ (the theoretical or philosophical study of numbers) is an indigenous tradition. Aside from a few fragments, most of what is known about Greek mathematics in the 6th to 4th centuries BC (the Archaic and Classical periods) comes through either the reports of contemporary non-mathematicians or references from mathematical works in the early Hellenistic period.[31] In the case of number theory, this means largely Plato, Aristotle, and Euclid.
Plato had a keen interest in mathematics, and distinguished clearly between arithmētikḗ and calculation (logistikē). Plato reports in his dialogue Theaetetus that Theodorus had proven that are irrational. Theaetetus, a disciple of Theodorus's, worked on distinguishing different kinds of incommensurables, and was thus arguably a pioneer in the study of number systems. Aristotle further claimed that the philosophy of Plato closely followed the teachings of the Pythagoreans,[32] and Cicero repeats this claim: Platonem ferunt didicisse Pythagorea omnia ("They say Plato learned all things Pythagorean").[33]
Euclid devoted part of his Elements (Books VII–IX) to topics that belong to elementary number theory, including prime numbers and divisibility.[34] He gave an algorithm, the Euclidean algorithm, for computing the greatest common divisor of two numbers (Prop. VII.2) and a proof implying the infinitude of primes (Prop. IX.20). There is also older material likely based on Pythagorean teachings (Prop. IX.21–34), such as "odd times even is even" and "if an odd number measures [= divides] an even number, then it also measures [= divides] half of it".[35] This is all that is needed to prove that is irrational.[36] Pythagoreans apparently gave great importance to the odd and the even.[37] The discovery that is irrational is credited to the early Pythagoreans, sometimes assigned to Hippasus, who was expelled or split from the Pythagorean community as a result.[38][39] This forced a distinction between numbers (integers and the rationals—the subjects of arithmetic) and lengths and proportions (which may be identified with real numbers, whether rational or not).
The Pythagorean tradition also spoke of so-called polygonal or figurate numbers.[40] While square numbers, cubic numbers, etc., are seen now as more natural than triangular numbers, pentagonal numbers, etc., the study of the sums of triangular and pentagonal numbers would prove fruitful in the early modern period (17th to early 19th centuries).
An epigram published by Lessing in 1773 appears to be a letter sent by Archimedes to Eratosthenes.[41] The epigram proposed what has become known as Archimedes's cattle problem; its solution (absent from the manuscript) requires solving an indeterminate quadratic equation (which reduces to what would later be misnamed Pell's equation). As far as it is known, such equations were first successfully treated by Indian mathematicians. It is not known whether Archimedes himself had a method of solution.
Late Antiquity
[edit]
Aside from the elementary work of Neopythagoreans such as Nicomachus and Theon of Smyrna, the foremost authority in arithmētikḗ in Late Antiquity was Diophantus of Alexandria, who probably lived in the 3rd century AD, approximately five hundred years after Euclid. Little is known about his life, but he wrote two works that are extant: On Polygonal Numbers, a short treatise written in the Euclidean manner on the subject, and the Arithmetica, a work on pre-modern algebra (namely, the use of algebra to solve numerical problems). Six out of the thirteen books of Diophantus's Arithmetica survive in the original Greek and four more survive in an Arabic translation. The Arithmetica is a collection of worked-out problems where the task is invariably to find rational solutions to a system of polynomial equations, usually of the form or . In modern parlance, Diophantine equations are polynomial equations to which rational or integer solutions are sought.
China
[edit]The Chinese remainder theorem appears as an exercise[42] in Sunzi Suanjing (between the third and fifth centuries).[43] (There is one important step glossed over in Sunzi's solution:[note 3] it is the problem that was later solved by Āryabhaṭa's Kuṭṭaka – see below.) The result was later generalized with a complete solution called Da-yan-shu (大衍術) in Qin Jiushao's 1247 Mathematical Treatise in Nine Sections[44] which was translated into English in early nineteenth century by British missionary Alexander Wylie.[45] There is also some numerical mysticism in Chinese mathematics,[note 4] but, unlike that of the Pythagoreans, it seems to have led nowhere.
India
[edit]While Greek astronomy probably influenced Indian learning, to the point of introducing trigonometry,[46] it seems to be the case that Indian mathematics is otherwise an autochthonous tradition;[47] in particular, there is no evidence that Euclid's Elements reached India before the eighteenth century.[48] Āryabhaṭa (476–550 AD) showed that pairs of simultaneous congruences , could be solved by a method he called kuṭṭaka, or pulveriser;[49] this is a procedure close to (a generalization of) the Euclidean algorithm, which was probably discovered independently in India.[50] Āryabhaṭa seems to have had in mind applications to astronomical calculations.[46]
Brahmagupta (628 AD) started the systematic study of indefinite quadratic equations—in particular, the misnamed Pell equation, in which Archimedes may have first been interested, and which did not start to be solved in the West until the time of Fermat and Euler. Later Sanskrit authors would follow, using Brahmagupta's technical terminology. A general procedure (the chakravala, or "cyclic method") for solving Pell's equation was finally found by Jayadeva (cited in the eleventh century; his work is otherwise lost); the earliest surviving exposition appears in Bhāskara II's Bīja-gaṇita (twelfth century).[51]
Indian mathematics remained largely unknown in Europe until the late eighteenth century;[52] Brahmagupta and Bhāskara's work was translated into English in 1817 by Henry Colebrooke.[53]
Arithmetic in the Islamic golden age
[edit]
In the early ninth century, the caliph al-Ma'mun ordered translations of many Greek mathematical works and at least one Sanskrit work (the Sindhind, which may[54] or may not[55] be Brahmagupta's Brāhmasphuṭasiddhānta). Diophantus's main work, the Arithmetica, was translated into Arabic by Qusta ibn Luqa (820–912). Part of the treatise al-Fakhri (by al-Karajī, 953 – c. 1029) builds on it to some extent. According to Rashed Roshdi, Al-Karajī's contemporary Ibn al-Haytham knew[56] what would later be called Wilson's theorem.
Around 1000 AD, the Islamic mathematician Ibn al-Haytham (Alhazen) found Wilson's theorem, characterizing the prime numbers as the numbers that evenly divide . He also conjectured that all even perfect numbers come from Euclid's construction using Mersenne primes, but was unable to prove it.[57] Another Islamic mathematician, Ibn al-Banna' al-Marrakushi, observed that the sieve of Eratosthenes can be sped up by considering only the prime divisors up to the square root of the upper limit.[27] Fibonacci took the innovations from Islamic mathematics to Europe. His book Liber Abaci (1202) was the first to describe trial division for testing primality, again using divisors only up to the square root.[27] a
Western Europe in the Middle Ages
[edit]Other than a treatise on squares in arithmetic progression by Fibonacci—who traveled and studied in north Africa and Constantinople—no number theory to speak of was done in western Europe during the Middle Ages. Matters started to change in Europe in the late Renaissance, thanks to a renewed study of the works of Greek antiquity. A catalyst was the textual emendation and translation into Latin of Diophantus' Arithmetica.[58]
Early modern number theory
[edit]Fermat
[edit]
Pierre de Fermat (1607–1665) never published his writings but communicated through correspondence instead. Accordingly, his work on number theory is contained almost entirely in letters to mathematicians and in private marginal notes.[59] Although he drew inspiration from classical sources, in his notes and letters Fermat scarcely wrote any proofs—he had no models in the area.[60]
The corpus of his works consists of letters sent in private correspondence and marginal notes, in which he often formulated conjectures.
In 1640 Pierre de Fermat stated (without proof) Fermat's little theorem (later proved by Leibniz and Euler).[61] Fermat also investigated the primality of the Fermat numbers ,[62] and Marin Mersenne studied the Mersenne primes, prime numbers of the form with itself a prime.[63]
Over his lifetime, Fermat made the following contributions to the field:
- One of Fermat's first interests was perfect numbers (which appear in Euclid, Elements IX) and amicable numbers;[note 5] these topics led him to work on integer divisors, which were from the beginning among the subjects of the correspondence (1636 onwards) that put him in touch with the mathematical community of the day.[64]
- In 1638, Fermat claimed, without proof, that all whole numbers can be expressed as the sum of four squares or fewer.[65]
- Fermat's little theorem (1640):[66] if a is not divisible by a prime p, then
- If a and b are coprime, then is not divisible by any prime congruent to −1 modulo 4;[67] and every prime congruent to 1 modulo 4 can be written in the form .[68] These two statements also date from 1640; in 1659, Fermat stated to Huygens that he had proven the latter statement by the method of infinite descent.[69]
- In 1657, Fermat posed the problem of solving as a challenge to English mathematicians. The problem was solved in a few months by Wallis and Brouncker.[70] Fermat considered their solution valid, but pointed out they had provided an algorithm without a proof (as had Jayadeva and Bhaskara, though Fermat was not aware of this). He stated that a proof could be found by infinite descent.
- Fermat stated and proved (by infinite descent) in the appendix to Observations on Diophantus (Obs. XLV)[71] that has no non-trivial solutions in the integers. Fermat also mentioned to his correspondents that has no non-trivial solutions, and that this could also be proven by infinite descent.[72] The first known proof is due to Euler (1753; indeed by infinite descent).[73]
- Fermat claimed (Fermat's Last Theorem) to have shown there are no solutions to for all ; this claim appears in his annotations in the margins of his copy of Diophantus.
Euler
[edit]
The interest of Leonhard Euler (1707–1783) in number theory was first spurred in 1729, when a friend of his, the amateur[note 6] Goldbach, pointed him towards some of Fermat's work on the subject.[74] This has been called the "rebirth" of modern number theory,[75] after Fermat's relative lack of success in getting his contemporaries' attention for the subject.[76] Euler's work on number theory includes the following:[77]
Christian Goldbach formulated Goldbach's conjecture, that every even number is the sum of two primes, in a 1742 letter to Euler.[78] Euler proved Alhazen's conjecture (now the Euclid–Euler theorem) that all even perfect numbers can be constructed from Mersenne primes.[25] He introduced methods from mathematical analysis to this area in his proofs of the infinitude of the primes and the divergence of the sum of the reciprocals of the primes .[79]
- Proofs for Fermat's statements. This includes Fermat's little theorem (generalised by Euler to non-prime moduli); the fact that if and only if ; initial work towards a proof that every integer is the sum of four squares (the first complete proof is by Joseph-Louis Lagrange (1770), soon improved by Euler himself[80]); the lack of non-zero integer solutions to (implying the case n=4 of Fermat's last theorem, the case n=3 of which Euler also proved by a related method).
- Pell's equation, first misnamed by Euler.[81] He wrote on the link between continued fractions and Pell's equation.[82]
- First steps towards analytic number theory. In his work of sums of four squares, partitions, pentagonal numbers, and the distribution of prime numbers, Euler pioneered the use of what can be seen as analysis (in particular, infinite series) in number theory. Since he lived before the development of complex analysis, most of his work is restricted to the formal manipulation of power series. He did, however, do some very notable (though not fully rigorous) early work on what would later be called the Riemann zeta function.[83]
- Quadratic forms. Following Fermat's lead, Euler did further research on the question of which primes can be expressed in the form , some of it prefiguring quadratic reciprocity.[84]
- Diophantine equations. Euler worked on some Diophantine equations of genus 0 and 1.[85] In particular, he studied Diophantus's work; he tried to systematise it, but the time was not yet ripe for such an endeavour—algebraic geometry was still in its infancy.[86] He did notice there was a connection between Diophantine problems and elliptic integrals,[86] whose study he had himself initiated.
Lagrange, Legendre, and Gauss
[edit]
At the start of the 19th century, Legendre and Gauss conjectured that as tends to infinity, the number of primes up to is asymptotic to , where is the natural logarithm of . A weaker consequence of this high density of primes was Bertrand's postulate, that for every there is a prime between and , proved in 1852 by Pafnuty Chebyshev.[87]
Joseph-Louis Lagrange (1736–1813) was the first to give full proofs of some of Fermat's and Euler's work and observations; for instance, the four-square theorem and the basic theory of the misnamed "Pell's equation" (for which an algorithmic solution was found by Fermat and his contemporaries, and also by Jayadeva and Bhaskara II before them.) He also studied quadratic forms in full generality (as opposed to ), including defining their equivalence relation, showing how to put them in reduced form, etc.
Adrien-Marie Legendre (1752–1833) was the first to state the law of quadratic reciprocity. He also conjectured what amounts to the prime number theorem and Dirichlet's theorem on arithmetic progressions. He gave a full treatment of the equation [88] and worked on quadratic forms along the lines later developed fully by Gauss.[89] In his old age, he was the first to prove Fermat's Last Theorem for (completing work by Peter Gustav Lejeune Dirichlet, and crediting both him and Sophie Germain).[90]
Carl Friedrich Gauss (1777–1855) worked in a wide variety of fields in both mathematics and physics including number theory, analysis, differential geometry, geodesy, magnetism, astronomy and optics. The Disquisitiones Arithmeticae (1801), which he wrote three years earlier when he was 21, had an immense influence in the area of number theory and set its agenda for much of the 19th century. Gauss proved in this work the law of quadratic reciprocity and developed the theory of quadratic forms (in particular, defining their composition). He also introduced some basic notation (congruences) and devoted a section to computational matters, including primality tests.[91] The last section of the Disquisitiones established a link between roots of unity and number theory:
The theory of the division of the circle...which is treated in sec. 7 does not belong by itself to arithmetic, but its principles can only be drawn from higher arithmetic.[92]
In this way, Gauss arguably made forays towards Évariste Galois's work and the area algebraic number theory.
Maturity and division into subfields
[edit]
Starting early in the nineteenth century, the following developments gradually took place:
- The rise to self-consciousness of number theory (or higher arithmetic) as a field of study.[93]
- The development of much of modern mathematics necessary for basic modern number theory: complex analysis, group theory, Galois theory—accompanied by greater rigor in analysis and abstraction in algebra.
- The rough subdivision of number theory into its modern subfields—in particular, analytic and algebraic number theory.
Ideas of Bernhard Riemann in his 1859 paper on the zeta-function sketched an outline for proving the conjecture of Legendre and Gauss. Although the closely related Riemann hypothesis remains unproven, Riemann's outline was completed in 1896 by Hadamard and de la Vallée Poussin, and the result is now known as the prime number theorem.[94] Another important 19th century result was Dirichlet's theorem on arithmetic progressions, that certain arithmetic progressions contain infinitely many primes.[95]
Many mathematicians have worked on primality tests for numbers larger than those where trial division is practicably applicable. Methods that are restricted to specific number forms include Pépin's test for Fermat numbers (1877),[96] Proth's theorem (c. 1878),[97] the Lucas–Lehmer primality test (originated 1856), and the generalized Lucas primality test.[27]
Algebraic number theory may be said to start with the study of reciprocity and cyclotomy, but truly came into its own with the development of abstract algebra and early ideal theory and valuation theory; see below. A conventional starting point for analytic number theory is Dirichlet's theorem on arithmetic progressions (1837),[98] whose proof introduced L-functions and involved some asymptotic analysis and a limiting process on a real variable.[99] The first use of analytic ideas in number theory actually goes back to Euler (1730s),[100] who used formal power series and non-rigorous (or implicit) limiting arguments. The use of complex analysis in number theory comes later: the work of Bernhard Riemann (1859) on the zeta function is the canonical starting point;[101] Jacobi's four-square theorem (1839), which predates it, belongs to an initially different strand that has by now taken a leading role in analytic number theory (modular forms).[102]
Pafnuty Chebyshev (1821-1894) provided substantiated cases for the PNT such as the existence of primes within specific intervals.
Information Age
[edit]Since 1951 all the largest known primes have been found using these tests on computers.[a] The search for ever larger primes has generated interest outside mathematical circles, through the Great Internet Mersenne Prime Search and other distributed computing projects.[104][105]
The American Mathematical Society awards the Cole Prize in Number Theory. Moreover, number theory is one of the three mathematical subdisciplines rewarded by the Fermat Prize.
The idea that prime numbers had few applications outside of pure mathematics[b] was shattered in the 1970s when public-key cryptography and the RSA cryptosystem were invented, using prime numbers as their basis.[108]
Number theory was once regarded as the canonical example of pure mathematics with no applications outside the field. In 1970s, it became known that prime numbers would be used as the basis for the creation of public-key cryptography algorithms. Schemes such as RSA are based on the difficulty of factoring large composite numbers into their prime factors. Elementary number theory is taught in discrete mathematics courses for computer scientists.
The increased practical importance of computerized primality testing and factorization led to the development of improved methods capable of handling large numbers of unrestricted form.[26][109][110] The mathematical theory of prime numbers also moved forward with the Green–Tao theorem (2004) that there are arbitrarily long arithmetic progressions of prime numbers, and Yitang Zhang's 2013 proof that there exist infinitely many prime gaps of bounded size.[111]
One quirk of number theory is that it deals with statements that are simple to understand but require a high degree of sophistication to solve. Open questions remain, such as the aforementioned Riemann hypothesis that is among the seven Millennium Prize Problems, Goldbach's conjecture on the representation of even numbers as the sum of two primes, and the existence of odd perfect numbers.
Historiography
[edit]Notes
[edit]- ^ The term 'arithmetic' may have regained some ground, arguably due to French influence. Take, for example, Serre 1996. In 1952, Davenport still had to specify that he meant The Higher Arithmetic. Hardy and Wright wrote in the introduction to An Introduction to the Theory of Numbers (1938): "We proposed at one time to change [the title] to An introduction to arithmetic, a more novel and in some ways a more appropriate title; but it was pointed out that this might lead to misunderstandings about the content of the book." (Hardy & Wright 2008)
- ^ Robson 2001, p. 201. This is controversial. See Plimpton 322. Robson's article is written polemically (Robson 2001, p. 202) with a view to "perhaps [...] knocking [Plimpton 322] off its pedestal" (Robson 2001, p. 167); at the same time, it settles to the conclusion that
Robson takes issue with the notion that the scribe who produced Plimpton 322 (who had to "work for a living", and would not have belonged to a "leisured middle class") could have been motivated by his own "idle curiosity" in the absence of a "market for new mathematics".(Robson 2001, pp. 199–200)[...] the question "how was the tablet calculated?" does not have to have the same answer as the question "what problems does the tablet set?" The first can be answered most satisfactorily by reciprocal pairs, as first suggested half a century ago, and the second by some sort of right-triangle problems (Robson 2001, p. 202).
- ^ Sunzi Suanjing, Ch. 3, Problem 26, in Lam & Ang 2004, pp. 219–220:
[26] Now there are an unknown number of things. If we count by threes, there is a remainder 2; if we count by fives, there is a remainder 3; if we count by sevens, there is a remainder 2. Find the number of things. Answer: 23. Method: If we count by threes and there is a remainder 2, put down 140. If we count by fives and there is a remainder 3, put down 63. If we count by sevens and there is a remainder 2, put down 30. Add them to obtain 233 and subtract 210 to get the answer. If we count by threes and there is a remainder 1, put down 70. If we count by fives and there is a remainder 1, put down 21. If we count by sevens and there is a remainder 1, put down 15. When [a number] exceeds 106, the result is obtained by subtracting 105.
- ^ See, for example, Sunzi Suanjing, Ch. 3, Problem 36, in Lam & Ang 2004, pp. 223–224:
This is the last problem in Sunzi's otherwise matter-of-fact treatise.[36] Now there is a pregnant woman whose age is 29. If the gestation period is 9 months, determine the sex of the unborn child. Answer: Male. Method: Put down 49, add the gestation period and subtract the age. From the remainder take away 1 representing the heaven, 2 the earth, 3 the man, 4 the four seasons, 5 the five phases, 6 the six pitch-pipes, 7 the seven stars [of the Dipper], 8 the eight winds, and 9 the nine divisions [of China under Yu the Great]. If the remainder is odd, [the sex] is male and if the remainder is even, [the sex] is female.
- ^ Perfect and especially amicable numbers are of little or no interest nowadays. The same was not true in earlier times—whether in the West or the Arab-speaking world—due in part to the importance given to them by the Neopythagorean Nicomachus (c. 100 AD), who wrote a very elementary but influential book entitled Introduction to Arithmetic. See van der Waerden 1961, Ch. IV.
- ^ Up to the second half of the seventeenth century, academic positions were very rare, and most mathematicians and scientists earned their living in some other way (Weil 1984, pp. 159, 161). (There were already some recognisable features of professional practice, viz., seeking correspondents, visiting foreign colleagues, building private libraries (Weil 1984, pp. 160–161). Matters started to shift in the late seventeenth century (Weil 1984, p. 161); scientific academies were founded in England (the Royal Society, 1662) and France (the Académie des sciences, 1666) and Russia (1724). Euler was offered a position at this last one in 1726; he accepted, arriving in St. Petersburg in 1727 (Weil 1984, p. 163 and Varadarajan 2006, p. 7). In this context, the term amateur usually applied to Goldbach is well-defined and makes some sense: he has been described as a man of letters who earned a living as a spy (Truesdell 1984, p. xv); cited in Varadarajan 2006, p. 9). Notice, however, that Goldbach published some works on mathematics and sometimes held academic positions.
References
[edit]- ^
- ^
- Romanowski 2008, p. 304
- Nagel 2002, pp. 180–181
- Hindry 2011, p. x
- Hafstrom 2013, p. 95
- ^
- ^
- ^
- Wilson 2020, pp. 1–2
- Karatsuba 2020
- Campbell 2012, p. 33
- Robbins 2006, p. 1
- ^
- Duverney 2010, p. v
- Robbins 2006, p. 1
- ^ Weisstein 2003, Number Theory, Whole Numbers
- ^ Effinger & Mullen 2022, Divisibility in the Integers Z
- ^ Watkins 2014, p. xi
- ^ Karatsuba 2020
- ^ Davenport 2008, Introduction
- ^ Ore 1948, p. 28
- ^
- Burgin 2022, pp. 2–3
- Ore 1948, pp. 1, 6, 8, 10
- Thiam & Rochon 2019, p. 164
- ^ Rudman 2007, pp. 62–65
- ^
- ^ Karatsuba 2020
- ^ Dunham 2025
- ^
- Burgin 2022, pp. 6–7, 9
- Ore 1948, pp. 16–18
- ITL Education Solutions Limited 2011, p. 28
- ^ Neugebauer & Sachs 1945, p. 40Robson 2001, p. 192
- ^ Watkins 2014, Number Theory Begins
- ^ Neugebauer (Neugebauer 1969, pp. 36–40) discusses the table in detail and mentions in passing Euclid's method in modern notation (Neugebauer 1969, p. 39).
- ^ Friberg 1981, p. 302.
- ^ van der Waerden 1961, p. 63-75.
- ^ Bruins, Evert Marie, review in Mathematical Reviews of Gillings, R.J. (1974). "The recto of the Rhind Mathematical Papyrus. How did the ancient Egyptian scribe prepare it?". Archive for History of Exact Sciences. 12 (4): 291–298. doi:10.1007/BF01307175. MR 0497458. S2CID 121046003.
- ^ a b Stillwell, John (2010). Mathematics and Its History. Undergraduate Texts in Mathematics (3rd ed.). Springer. p. 40. ISBN 978-1-4419-6052-8.
- ^ a b Pomerance, Carl (December 1982). "The Search for Prime Numbers". Scientific American. 247 (6): 136–147. Bibcode:1982SciAm.247f.136P. doi:10.1038/scientificamerican1282-136. JSTOR 24966751.
- ^ a b c d Mollin, Richard A. (2002). "A brief history of factoring and primality testing B. C. (before computers)". Mathematics Magazine. 75 (1): 18–29. doi:10.2307/3219180. JSTOR 3219180. MR 2107288.
- ^ van der Waerden 1961, p. 87-90
- ^ Iamblichus, Life of Pythagoras,(trans., for example, Guthrie 1987) cited in van der Waerden 1961, p. 108. See also Porphyry, Life of Pythagoras, paragraph 6, in Guthrie 1987
- ^ Herodotus (II. 81) and Isocrates (Busiris 28), cited in: Huffman 2011. On Thales, see Eudemus ap. Proclus, 65.7, (for example, Morrow 1992, p. 52) cited in: O'Grady 2004, p. 1. Proclus was using a work by Eudemus of Rhodes (now lost), the Catalogue of Geometers. See also introduction, Morrow 1992, p. xxx on Proclus's reliability.
- ^ Boyer & Merzbach 1991, p. 82.
- ^ Metaphysics, 1.6.1 (987a)
- ^ Tusc. Disput. 1.17.39.
- ^ Corry 2015, Construction Problems and Numerical Problems in the Greek Mathematical Tradition
- ^ Becker 1936, p. 533, cited in: van der Waerden 1961, p. 108.
- ^ Becker 1936.
- ^ van der Waerden 1961, p. 109.
- ^ Plato, Theaetetus, p. 147 B, (for example, Jowett 1871), cited in von Fritz 2004, p. 212: "Theodorus was writing out for us something about roots, such as the roots of three or five, showing that they are incommensurable by the unit;..." See also Spiral of Theodorus.
- ^ von Fritz 2004.
- ^ Heath 1921, p. 76.
- ^ Vardi 1998, pp. 305–319.
- ^ Sunzi Suanjing, Chapter 3, Problem 26. This can be found in Lam & Ang 2004, pp. 219–220, which contains a full translation of the Suan Ching (based on Qian 1963). See also the discussion in Lam & Ang 2004, pp. 138–140.
- ^ The date of the text has been narrowed down to 220–420 AD (Yan Dunjie) or 280–473 AD (Wang Ling) through internal evidence (= taxation systems assumed in the text). See Lam & Ang 2004, pp. 27–28.
- ^ Dauben 2007, p. 310
- ^ Libbrecht 1973
- ^ a b Plofker 2008, p. 119.
- ^ Any early contact between Babylonian and Indian mathematics remains conjectural (Plofker 2008, p. 42).
- ^ Mumford 2010, p. 387.
- ^ Āryabhaṭa, Āryabhatīya, Chapter 2, verses 32–33, cited in: Plofker 2008, pp. 134–140. See also Aryabhata 1930, pp. 42–50. A slightly more explicit description of the kuṭṭaka was later given in Brahmagupta, Brāhmasphuṭasiddhānta, XVIII, 3–5 (in Colebrooke 1817, p. 325, cited in Aryabhata 1930, p. 42).
- ^ Mumford 2010, p. 388.
- ^ Plofker 2008, p. 194.
- ^ Plofker 2008, p. 283.
- ^ Colebrooke 1817.
- ^ Colebrooke 1817, p. lxv, cited in Hopkins 1990, p. 302. See also the preface in Sachau & Bīrūni 1888 cited in Smith 1958, pp. 168
- ^ Pingree 1968, pp. 97–125, and Pingree 1970, pp. 103–123, cited in Plofker 2008, p. 256.
- ^ Rashed 1980, pp. 305–321.
- ^ O'Connor, John J.; Robertson, Edmund F. "Abu Ali al-Hasan ibn al-Haytham". MacTutor History of Mathematics Archive. University of St Andrews.
- ^ Bachet, 1621, following a first attempt by Xylander, 1575
- ^ Weil 1984, pp. 45–46.
- ^ Weil 1984, p. 118. This was more so in number theory than in other areas (Mahoney 1994, pp. 283–289). Bachet's own proofs were "ludicrously clumsy" (Weil 1984, p. 33).
- ^ Sandifer 2007, 8. Fermat's Little Theorem (November 2003), p. 45
- ^ Sandifer, C. Edward (2014). How Euler Did Even More. Mathematical Association of America. p. 42. ISBN 978-0-88385-584-3.
- ^ Koshy, Thomas (2002). Elementary Number Theory with Applications. Academic Press. p. 369. ISBN 978-0-12-421171-1.
- ^ Mahoney 1994, pp. 48, 53–54. The initial subjects of Fermat's correspondence included divisors ("aliquot parts") and many subjects outside number theory; see the list in the letter from Fermat to Roberval, 22.IX.1636, Tannery & Henry 1891, Vol. II, pp. 72, 74, cited in Mahoney 1994, p. 54.
- ^ Faulkner, Nicholas; Hosch, William L. (2017). "Numbers and Measurements". Encyclopaedia Britannica. ISBN 978-1-5383-0042-8. Retrieved 2019-08-06.
- ^ Tannery & Henry 1891, Vol. II, p. 209, Letter XLVI from Fermat to Frenicle, 1640, cited in Weil 1984, p. 56
- ^ Tannery & Henry 1891, Vol. II, p. 204, cited in Weil 1984, p. 63. All of the following citations from Fermat's Varia Opera are taken from Weil 1984, Chap. II. The standard Tannery & Henry work includes a revision of Fermat's posthumous Varia Opera Mathematica originally prepared by his son (Fermat 1679).
- ^ Tannery & Henry 1891, Vol. II, p. 213.
- ^ Tannery & Henry 1891, Vol. II, p. 423.
- ^ Weil 1984, p. 92.
- ^ Tannery & Henry 1891, Vol. I, pp. 340–341.
- ^ Weil 1984, p. 115.
- ^ Weil 1984, pp. 115–116.
- ^ Weil 1984, pp. 2, 172.
- ^ Weil 1984, pp. 1–2.
- ^ Weil 1984, p. 2 and Varadarajan 2006, p. 37
- ^ Varadarajan 2006, p. 39 and Weil 1984, pp. 176–189
- ^ Yuan, Wang (2002). Goldbach Conjecture. Series In Pure Mathematics. Vol. 4 (2nd ed.). World Scientific. p. 21. ISBN 978-981-4487-52-8.
- ^ Narkiewicz, Wladyslaw (2000). "1.2 Sum of Reciprocals of Primes". The Development of Prime Number Theory: From Euclid to Hardy and Littlewood. Springer Monographs in Mathematics. Springer. p. 11. ISBN 978-3-540-66289-1.
- ^ Weil 1984, pp. 178–179.
- ^ Weil 1984, p. 174. Euler was generous in giving credit to others (Varadarajan 2006, p. 14), not always correctly.
- ^ Weil 1984, p. 183.
- ^ Varadarajan 2006, pp. 45–55; see also chapter III.
- ^ Varadarajan 2006, pp. 44–47.
- ^ Varadarajan 2006, pp. 55–56.
- ^ a b Weil 1984, p. 181.
- ^ Tchebychev, P. (1852). "Mémoire sur les nombres premiers" (PDF). Journal de mathématiques pures et appliquées. Série 1 (in French): 366–390.. (Proof of the postulate: 371–382). Also see Mémoires de l'Académie Impériale des Sciences de St. Pétersbourg, vol. 7, pp. 15–33, 1854
- ^ Weil 1984, pp. 327–328.
- ^ Weil 1984, pp. 332–334.
- ^ Weil 1984, pp. 337–338.
- ^ Goldstein & Schappacher 2007, p. 14.
- ^ From the preface of Disquisitiones Arithmeticae; the translation is taken from Goldstein & Schappacher 2007, p. 16
- ^ See the discussion in section 5 of Goldstein & Schappacher 2007. Early signs of self-consciousness are present already in letters by Fermat: thus his remarks on what number theory is, and how "Diophantus's work [...] does not really belong to [it]" (quoted in Weil 1984, p. 25).
- ^ Apostol, Tom M. (2000). "A centennial history of the prime number theorem". In Bambah, R.P.; Dumir, V.C.; Hans-Gill, R.J. (eds.). Number Theory. Trends in Mathematics. Basel: Birkhäuser. pp. 1–14. MR 1764793.
- ^ Apostol, Tom M. (1976). "7. Dirichlet's Theorem on Primes in Arithmetical Progressions". Introduction to Analytic Number Theory. New York; Heidelberg: Springer-Verlag. pp. 146–156. MR 0434929.
- ^ Chabert, Jean-Luc (2012). A History of Algorithms: From the Pebble to the Microchip. Springer. p. 261. ISBN 978-3-642-18192-4.
- ^ Rosen, Kenneth H. (2000). "Theorem 9.20. Proth's Primality Test". Elementary Number Theory and Its Applications (4th ed.). Addison-Wesley. p. 342. ISBN 978-0-201-87073-2.
- ^ Apostol 1976, p. 7. sfn error: multiple targets (2×): CITEREFApostol1976 (help)
- ^ See the proof in Davenport & Montgomery 2000, section 1
- ^ Iwaniec & Kowalski 2004, p. 1.
- ^ Granville 2008, pp. 322–348.
- ^ See the comment on the importance of modularity in Iwaniec & Kowalski 2004, p. 1
- ^ Cooper, S. Barry; Hodges, Andrew (2016). The Once and Future Turing. Cambridge University Press. pp. 37–38. ISBN 978-1-107-01083-3.
- ^ Cite error: The named reference
zieglerwas invoked but never defined (see the help page). - ^ Rosen 2000, p. 245.
- ^ Beiler, Albert H. (1999) [1966]. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. Dover. p. 2. ISBN 978-0-486-21096-4. OCLC 444171535.
- ^ Katz, Shaul (2004). "Berlin roots – Zionist incarnation: the ethos of pure mathematics and the beginnings of the Einstein Institute of Mathematics at the Hebrew University of Jerusalem". Science in Context. 17 (1–2): 199–234. doi:10.1017/S0269889704000092. MR 2089305. S2CID 145575536.
- ^ Kraft, James S.; Washington, Lawrence C. (2014). Elementary Number Theory. Textbooks in mathematics. CRC Press. p. 7. ISBN 978-1-4987-0269-0.
- ^ Bauer, Craig P. (2013). Secret History: The Story of Cryptology. Discrete Mathematics and Its Applications. CRC Press. p. 468. ISBN 978-1-4665-6186-1.
- ^ Klee, Victor; Wagon, Stan (1991). Old and New Unsolved Problems in Plane Geometry and Number Theory. Dolciani mathematical expositions. Vol. 11. Cambridge University Press. p. 224. ISBN 978-0-88385-315-3.
- ^ Neale 2017, pp. 18, 47.
Sources
[edit]- Apostol, Tom M. (1976). Introduction to analytic number theory. Undergraduate Texts in Mathematics. Springer. ISBN 978-0-387-90163-3. Retrieved 2016-02-28.
- Apostol, Tom M. (1981). "An Introduction to the Theory of Numbers (Review of Hardy & Wright.)". Mathematical Reviews (MathSciNet). American Mathematical Society. MR 0568909. (Subscription needed)
- Aryabhata (1930). The Āryabhaṭīya of Āryabhaṭa: An ancient Indian work on Mathematics and Astronomy. Translated by Clark, Walter Eugene. University of Chicago Press. Retrieved 2016-02-28.
- Becker, Oskar (1936). "Die Lehre von Geraden und Ungeraden im neunten Buch der euklidischen Elemente". Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik. Abteilung B:Studien (in German). 3: 533–553.
- Boyer, Carl Benjamin; Merzbach, Uta C. (1991) [1968]. A History of Mathematics (2nd ed.). New York: Wiley. ISBN 978-0-471-54397-8. 1968 edition at archive.org
- Bukhshtab, A. A.; Nechaev, V. I. (2016). "Natural Number". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
- Bukhshtab, A. A.; Pechaev, V. I. (2020). "Arithmetic". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
- Burgin, Mark (2022). Trilogy Of Numbers And Arithmetic - Book 1: History Of Numbers And Arithmetic: An Information Perspective. World Scientific. ISBN 978-981-12-3685-3.
- Campbell, Stephen R. (2012). "Understanding Elementary Number Theory in Relation to Arithmetic and Algebra". In Zazkis, Rina; Campbell, Stephen R. (eds.). Number Theory in Mathematics Education: Perspectives and Prospects. Routledge. ISBN 978-1-136-50143-2.
- Colebrooke, Henry Thomas (1817). Algebra, with Arithmetic and Mensuration, from the Sanscrit of Brahmegupta and Bháscara. London: J. Murray. Retrieved 2016-02-28.
- Corry, Leo (2015). A Brief History of Numbers. Oxford University Press. ISBN 978-0-19-870259-7.
- Dauben, Joseph W. (2007), "Chapter 3: Chinese Mathematics", in Katz, Victor J. (ed.), The Mathematics of Egypt, Mesopotamia, China, India and Islam : A Sourcebook, Princeton University Press, pp. 187–384, ISBN 978-0-691-11485-9
- Davenport, Harold; Montgomery, Hugh L. (2000). Multiplicative Number Theory. Graduate Texts in Mathematics. Vol. 74 (revised 3rd ed.). Springer. ISBN 978-0-387-95097-6.
- Davenport, H. (2008). The Higher Arithmetic: An Introduction to the Theory of Numbers (8th ed.). Cambridge University Press. ISBN 978-0-511-45555-1.
- Dunham, William (12 March 2025). "Number theory". Britannica. Retrieved 21 June 2025.
- Duverney, Daniel (2010). Number Theory: An Elementary Introduction Through Diophantine Problems. World Scientific. ISBN 978-981-4307-46-8.
- Edwards, Harold M. (November 1983). "Euler and Quadratic Reciprocity". Mathematics Magazine. 56 (5): 285–291. doi:10.2307/2690368. JSTOR 2690368.
- Edwards, Harold M. (2000) [1977]. Fermat's Last Theorem: a Genetic Introduction to Algebraic Number Theory. Graduate Texts in Mathematics. Vol. 50 (reprint of 1977 ed.). Springer Verlag. ISBN 978-0-387-95002-0.
- Effinger, Gove; Mullen, Gary L. (2022). Elementary Number Theory. Boca Raton: CRC Press. ISBN 978-1-003-19311-1.
- Fermat, Pierre de (1679). Varia Opera Mathematica (in French and Latin). Toulouse: Joannis Pech. Retrieved 2016-02-28.
- Friberg, Jöran (August 1981). "Methods and Traditions of Babylonian Mathematics: Plimpton 322, Pythagorean Triples and the Babylonian Triangle Parameter Equations". Historia Mathematica. 8 (3): 277–318. doi:10.1016/0315-0860(81)90069-0.
- von Fritz, Kurt (2004). "The Discovery of Incommensurability by Hippasus of Metapontum". In Christianidis, J. (ed.). Classics in the History of Greek Mathematics. Berlin: Kluwer (Springer). ISBN 978-1-4020-0081-2.
- Gauss, Carl Friedrich (1966) [1801]. Disquisitiones Arithmeticae. Translated by Waterhouse, William C. Springer. ISBN 978-0-387-96254-2.
- Goldfeld, Dorian M. (2003). "Elementary Proof of the Prime Number Theorem: a Historical Perspective" (PDF). Archived (PDF) from the original on 2016-03-03. Retrieved 2016-02-28.
- Goldstein, Catherine; Schappacher, Norbert (2007). "A book in search of a discipline". In Goldstein, C.; Schappacher, N.; Schwermer, Joachim (eds.). The Shaping of Arithmetic after C.F. Gauss's "Disquisitiones Arithmeticae". Berlin & Heidelberg: Springer. pp. 3–66. ISBN 978-3-540-20441-1. Retrieved 2016-02-28.
- Granville, Andrew (2008). "Analytic number theory". In Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.). The Princeton Companion to Mathematics. Princeton University Press. ISBN 978-0-691-11880-2. Retrieved 2016-02-28.
- Grigorieva, Ellina (2018). Methods of Solving Number Theory Problems. Birkhäuser. ISBN 978-3-319-90915-8.
- Porphyry (1920). Life of Pythagoras. Translated by Guthrie, K. S. Alpine, New Jersey: Platonist Press. Archived from the original on 2020-02-29. Retrieved 2012-04-10.
- Guthrie, Kenneth Sylvan (1987). The Pythagorean Sourcebook and Library. Grand Rapids, Michigan: Phanes Press. ISBN 978-0-933999-51-0.
- Hafstrom, John Edward (2013). Basic Concepts in Modern Mathematics. Courier Corporation. ISBN 978-0-486-31627-7.
- Hardy, Godfrey Harold; Wright, E. M. (2008) [1938]. An Introduction to the Theory of Numbers (6th ed.). Oxford University Press. ISBN 978-0-19-921986-5. MR 2445243.
- HC staff (2022b). "Arithmetic". American Heritage Dictionary. HarperCollins. Retrieved 19 October 2023.
- Heath, Thomas L. (1921). A History of Greek Mathematics, Volume 1: From Thales to Euclid. Oxford: Clarendon Press. Retrieved 2016-02-28.
- Hindry, Marc (2011). Arithmetics. Universitext. Springer. doi:10.1007/978-1-4471-2131-2. ISBN 978-1-4471-2130-5.
- Hopkins, J. F. P. (1990). "Geographical and Navigational Literature". In Young, M. J. L.; Latham, J. D.; Serjeant, R. B. (eds.). Religion, Learning and Science in the 'Abbasid Period. The Cambridge history of Arabic literature. Cambridge University Press. ISBN 978-0-521-32763-3.
- Huffman, Carl A. (8 August 2011). "Pythagoras". In Zalta, Edward N. (ed.). Stanford Encyclopaedia of Philosophy (Fall 2011 ed.). Archived from the original on 2 December 2013. Retrieved 7 February 2012.
- ITL Education Solutions Limited (2011). Introduction to Computer Science. Pearson Education India. ISBN 978-81-317-6030-7.
- Iwaniec, Henryk; Kowalski, Emmanuel (2004). Analytic Number Theory. American Mathematical Society Colloquium Publications. Vol. 53. Providence, RI: American Mathematical Society. ISBN 978-0-8218-3633-0.
- Plato (1871). Theaetetus. Translated by Jowett, Benjamin. Archived from the original on 2011-07-09. Retrieved 2012-04-10.
- Karatsuba, A.A. (2020). "Number theory". Encyclopedia of Mathematics. Springer. Retrieved 2025-05-03.
{{cite web}}: CS1 maint: url-status (link) - Lam, Lay Yong; Ang, Tian Se (2004). Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in Ancient China (revised ed.). Singapore: World Scientific. ISBN 978-981-238-696-0. Retrieved 2016-02-28.
- Libbrecht, Ulrich (1973), Chinese Mathematics in the Thirteenth Century: the "Shu-shu Chiu-chang" of Ch'in Chiu-shao, Dover Publications Inc, ISBN 978-0-486-44619-6
- Long, Calvin T. (1972). Elementary Introduction to Number Theory (2nd ed.). Lexington, VA: D.C. Heath and Company. LCCN 77171950.
- Lozano-Robledo, Álvaro (2019). Number Theory and Geometry: An Introduction to Arithmetic Geometry. American Mathematical Soc. ISBN 978-1-4704-5016-8.
- Mahoney, M. S. (1994). The Mathematical Career of Pierre de Fermat, 1601–1665 (Reprint, 2nd ed.). Princeton University Press. ISBN 978-0-691-03666-3. Retrieved 2016-02-28.
- Milne, J. S. (18 March 2017). "Algebraic Number Theory". Retrieved 7 April 2020.
- Montgomery, Hugh L.; Vaughan, Robert C. (2007). Multiplicative Number Theory: I, Classical Theory. Cambridge University Press. ISBN 978-0-521-84903-6. Retrieved 2016-02-28.
- Moore, Patrick (2004). "Number theory". In Lerner, K. Lee; Lerner, Brenda Wilmoth (eds.). The Gale Encyclopedia of Science. Vol. 4 (3rd ed.). Gale. ISBN 0-7876-7559-8.
- Euclid; Proclus (1992). A Commentary on Book 1 of Euclid's Elements. Translated by Morrow, Glenn Raymond. Princeton University Press. ISBN 978-0-691-02090-7.
- Mumford, David (March 2010). "Mathematics in India: reviewed by David Mumford" (PDF). Notices of the American Mathematical Society. 57 (3): 387. ISSN 1088-9477. Archived (PDF) from the original on 2021-05-06. Retrieved 2021-04-28.
- MW staff (2023). "Definition of Arithmetic". www.merriam-webster.com. Retrieved 19 October 2023.
- Nagel, Rob (2002). U-X-L Encyclopedia of Science. U-X-L. ISBN 978-0-7876-5440-5.
- Nagel, Ernest; Newman, James Roy (2008). Godel's Proof. NYU Press. ISBN 978-0-8147-5837-3.
- Neugebauer, Otto E. (1969). The Exact Sciences in Antiquity. Vol. 9. New York: Dover Publications. ISBN 978-0-486-22332-2.
- Neugebauer, Otto E.; Sachs, Abraham Joseph; Götze, Albrecht (1945). Mathematical Cuneiform Texts. American Oriental Series. Vol. 29. American Oriental Society etc.
- Ore, Øystein (1948). Number Theory and Its History. McGraw-Hill. Dover reprint, 1988, ISBN 978-0-486-65620-5.
- Page, Robert L. (2003). "Number Theory, Elementary". Encyclopedia of Physical Science and Technology (Third ed.). Academic Press. ISBN 978-0-12-227410-7.
- O'Grady, Patricia (September 2004). "Thales of Miletus". The Internet Encyclopaedia of Philosophy. Archived from the original on 6 January 2016. Retrieved 7 February 2012.
- Pingree, David; Ya'qub, ibn Tariq (1968). "The Fragments of the Works of Ya'qub ibn Tariq". Journal of Near Eastern Studies. 26.
- Pingree, D.; al-Fazari (1970). "The Fragments of the Works of al-Fazari". Journal of Near Eastern Studies. 28.
- Plofker, Kim (2008). Mathematics in India. Princeton University Press. ISBN 978-0-691-12067-6.
- Ponticorvo, Michela; Schmbri, Massimiliano; Miglino, Orazio (2019). "How to Improve Spatial and Numerical Cognition with a Game-Based and Technology-Enhanced Learning Approach". In Vicente, José Manuel Ferrández; Álvarez-Sánchez, José Ramón; López, Félix de la Paz; Moreo, Javier Toledo; Adeli, Hojjat (eds.). Understanding the Brain Function and Emotions: 8th International Work-Conference on the Interplay Between Natural and Artificial Computation, IWINAC 2019, Almería, Spain, June 3–7, 2019, Proceedings, Part I. Springer. ISBN 978-3-030-19591-5.
- Qian, Baocong, ed. (1963). Suanjing shi shu (Ten Mathematical Classics) (in Chinese). Beijing: Zhonghua shuju. Archived from the original on 2013-11-02. Retrieved 2016-02-28.
- Rashed, Roshdi (1980). "Ibn al-Haytham et le théorème de Wilson". Archive for History of Exact Sciences. 22 (4): 305–321. doi:10.1007/BF00717654. S2CID 120885025.
- Robbins, Neville (2006). Beginning Number Theory. Jones & Bartlett Learning. ISBN 978-0-7637-3768-9.
- Robson, Eleanor (2001). "Neither Sherlock Holmes nor Babylon: a Reassessment of Plimpton 322" (PDF). Historia Mathematica. 28 (3): 167–206. doi:10.1006/hmat.2001.2317. Archived from the original (PDF) on 2014-10-21.
- Romanowski, Perry (2008). "Arithmetic". In Lerner, Brenda Wilmoth; Lerner, K. Lee (eds.). The Gale Encyclopedia of Science (4th ed.). Thompson Gale. ISBN 978-1-4144-2877-2.
- [1]
- Sachau, Eduard; Bīrūni, ̄Muḥammad ibn Aḥmad (1888). Alberuni's India: An Account of the Religion, Philosophy, Literature, Geography, Chronology, Astronomy and Astrology of India, Vol. 1. London: Kegan, Paul, Trench, Trübner & Co. Archived from the original on 2016-03-03. Retrieved 2016-02-28.
- Serre, Jean-Pierre (1996) [1973]. A Course in Arithmetic. Graduate Texts in Mathematics. Vol. 7. Springer. ISBN 978-0-387-90040-7.
- Smith, D. E. (1958). History of Mathematics, Vol I. New York: Dover.
- Tannery, Paul; Fermat, Pierre de (1891). Charles Henry (ed.). Oeuvres de Fermat. (4 Vols.) (in French and Latin). Paris: Imprimerie Gauthier-Villars et Fils. Volume 1 Volume 2 Volume 3 Volume 4 (1912)
- Tanton, James (2005). "Number theory". Encyclopedia of Mathematics. New York: Facts On File. ISBN 0-8160-5124-0.
- Iamblichus (1818). Life of Pythagoras or, Pythagoric Life. Translated by Taylor, Thomas. London: J. M. Watkins. For other editions, see Iamblichus#List of editions and translations
- Thiam, Thierno; Rochon, Gilbert (2019). Sustainability, Emerging Technologies, and Pan-Africanism. Springer Nature. ISBN 978-3-030-22180-5.
- Truesdell, C. A. (1984). "Leonard Euler, Supreme Geometer". Leonard Euler, Elements of Algebra. Translated by Hewlett, John (reprint of 1840 5th ed.). New York: Springer-Verlag. ISBN 978-0-387-96014-2. This Google books preview of Elements of algebra lacks Truesdell's intro, which is reprinted (slightly abridged) in the following book:
- Truesdell, C. A. (2007). "Leonard Euler, Supreme Geometer". In Dunham, William (ed.). The Genius of Euler: reflections on his life and work. Volume 2 of MAA tercentenary Euler celebration. New York: Mathematical Association of America. ISBN 978-0-88385-558-4. Retrieved 2016-02-28.
- Varadarajan, V. S. (2006). Euler Through Time: A New Look at Old Themes. American Mathematical Society. ISBN 978-0-8218-3580-7. Retrieved 2016-02-28.
- Vardi, Ilan (April 1998). "Archimedes' Cattle Problem" (PDF). American Mathematical Monthly. 105 (4): 305–319. CiteSeerX 10.1.1.383.545. doi:10.2307/2589706. JSTOR 2589706. Archived (PDF) from the original on 2012-07-15. Retrieved 2012-04-08.
- van der Waerden, Bartel L. (1961). Science Awakening. Vol. 1 or 2. Translated by Dresden, Arnold. New York: Oxford University Press.
- Watkins, John J. (2014). Number Theory: A Historical Approach. Princeton University Press. ISBN 978-0-691-15940-9.
- Weil, André (1984). Number Theory: an Approach Through History – from Hammurapi to Legendre. Boston: Birkhäuser. ISBN 978-0-8176-3141-3. Retrieved 2016-02-28.
- Weisstein, Eric W. (2003). CRC Concise Encyclopedia of Mathematics (2nd ed.). Chapman & Hall/CRC. ISBN 1-58488-347-2.
- Wilson, Robin (2020). Number Theory: A Very Short Introduction. Oxford University Press. ISBN 978-0-19-879809-5.
- This article incorporates material from the Citizendium article "History of number theory", which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.
Cite error: There are <ref group=lower-alpha> tags or {{efn}} templates on this page, but the references will not show without a {{reflist|group=lower-alpha}} template or {{notelist}} template (see the help page).
- ^ Rudman, Peter S. (2007). How Mathematics Happened: The First 50,000 Years. New York: Prometheus Books. ISBN 978-1-59102-477-4.







































