Ducci sequence

A Ducci sequence is a sequence of n-tuples of integers, sometimes known as "the Diffy game", because it is based on sequences.

Given an n-tuple of integers $(a_{1},a_{2},...,a_{n})$, the next n-tuple in the sequence is formed by taking the absolute differences of neighbouring integers:

$(a_{1},a_{2},...,a_{n})\rightarrow (|a_{1}-a_{2}|,|a_{2}-a_{3}|,...,|a_{n}-a_{1}|)\,.$

Another way of describing this is as follows. Arrange n integers in a circle and make a new circle by taking the difference between neighbours, ignoring any minus signs; then repeat the operation. Ducci sequences are named after Enrico Ducci (1864–1940), the Italian mathematician who discovered in the 1930s that every such sequence eventually becomes periodic.

Ducci sequences are also known as the Ducci map or the n-number game. Open problems in the study of these maps still remain.

Properties

From the second n-tuple onwards, it is clear that every integer in each n-tuple in a Ducci sequence is greater than or equal to 0 and is less than or equal to the difference between the maximum and minimum members of the first n-tuple. As there are only a finite number of possible n-tuples with these constraints, the sequence of n-tuples must sooner or later repeat itself. Every Ducci sequence therefore eventually becomes periodic.

If n is a power of 2 every Ducci sequence eventually reaches the n-tuple (0,0,...,0) in a finite number of steps.

If n is not a power of two, a Ducci sequence will either eventually reach an n-tuple of zeros or will settle into a periodic loop of 'binary' n-tuples; that is, n-tuples of form $k(b_{1},b_{2},...b_{n})$, $k$ is a constant, and $b_{i}\in \{0,1\}$.

An obvious generalisation of Ducci sequences is to allow the members of the n-tuples to be any real numbers rather than just integers. For example, this 4-tuple converges to (0, 0, 0, 0) in four iterations: $(e,\pi ,{\sqrt {2}},1)\rightarrow (\pi -e,\pi -{\sqrt {2}},{\sqrt {2}}-1,e-1)\rightarrow (e-{\sqrt {2}},\pi -2{\sqrt {2}}+1,e-{\sqrt {2}},2e-\pi -1)\rightarrow$ $(\pi -e-{\sqrt {2}}+1,\pi -e-{\sqrt {2}}+1,\pi -e-{\sqrt {2}}+1,\pi -e-{\sqrt {2}}+1)\rightarrow (0,0,0,0)$

The properties presented here do not always hold for these generalisations. For example, a Ducci sequence starting with the n-tuple (1, q, q², q³) where q is the (irrational) positive root of the cubic $x^{3}-x^{2}-x-1=0$ does not reach (0,0,0,0) in a finite number of steps, although in the limit it converges to (0,0,0,0).

Examples

Ducci sequences may be arbitrarily long before they reach a tuple of zeros or a periodic loop. The 4-tuple sequence starting with (0, 653, 1854, 4063) takes 24 iterations to reach the zeros tuple.

$(0,653,1854,4063)\rightarrow (653,1201,2209,4063)\rightarrow (548,1008,1854,3410)\rightarrow$ $\cdots \rightarrow (0,0,128,128)\rightarrow (0,128,0,128)\rightarrow (128,128,128,128)\rightarrow (0,0,0,0)$

This 5-tuple sequence enters a period 15 binary 'loop' after 7 iterations.

${\begin{matrix}15799\rightarrow &42208\rightarrow &20284\rightarrow &22642\rightarrow &04220\rightarrow &42020\rightarrow \\22224\rightarrow &00022\rightarrow &00202\rightarrow &02222\rightarrow &20002\rightarrow &20020\rightarrow \\20222\rightarrow &22000\rightarrow &02002\rightarrow &22022\rightarrow &02200\rightarrow &20200\rightarrow \\22202\rightarrow &00220\rightarrow &02020\rightarrow &22220\rightarrow &00022\rightarrow &\cdots \quad \quad \\\end{matrix}}$

The following 6-tuple sequence shows that sequences of tuples whose length is not a power of two may still reach a tuple of zeros:

${\begin{matrix}121210\rightarrow &111111\rightarrow &000000\\\end{matrix}}$

If some conditions are imposed on any "power of two"-tuple Ducci sequence, it would take that power of two or lesser iterations to reach the zeros tuple. It is hypothesized that these sequences conform to a rule.

Modulo two form

When the Ducci sequences enter binary loops, it is possible to treat the sequence in modulo two. That is:

$(|a_{1}-a_{2}|,|a_{2}-a_{3}|,...,|a_{n}-a_{1}|)\ =(a_{1}+a_{2},a_{2}+a_{3},...,a_{n}+a_{1}){\bmod {2}}$

This forms the basis for proving when the sequence vanish to all zeros.

Cellular automata

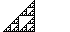
The linear map in modulo 2 can further be identified as the cellular automata denoted as rule 102 in Wolfram code and related to rule 90 through the Martin-Odlyzko-Wolfram map. Rule 102 reproduces the Sierpinski triangle.

Other related topics

The Ducci map is an example of a difference equation, a category that also include non-linear dynamics, chaos theory and numerical analysis. Similarities to cyclotomic polynomials have also been pointed out. While there are no practical applications of the Ducci map at present, its connection to the highly applied field of difference equations led to conjecture that a form of the Ducci map may also find application in the future.

External links

• Ducci Sequence Archived 2004-08-26 at the Wayback Machine
• Integer Iterations on a Circle at Cut-the-Knot