Ancient Greek mathematics

An illustration of Euclid's proof of the Pythagorean theorem

Ancient Greek mathematics refers to the history of mathematical ideas and texts in Ancient Greece during Classical and Late antiquity, mostly from the 5th century BC to the 6th century AD. Greek mathematicians lived in cities spread around the shores of the ancient Mediterranean, from Anatolia to Italy and North Africa, but were united by Greek culture and the Greek language. The development of mathematics as a theoretical discipline and the use of deductive reasoning in proofs is an important difference between Greek mathematics and those of preceding civilizations, such as Ancient Egypt and Babylonia.

The early history of Greek mathematics is obscure, and traditional narratives of mathematical theorems found before the fifth century BC are regarded as later inventions. It is now generally accepted that treatises of deductive mathematics written in Greek began circulating around the mid-fifth century BC, but the earliest complete work on the subject is the Elements, written during the Hellenistic period. The works of renown mathematicians Archimedes and Apollonius, as well as of the astronomer Hipparchus, also belong to this period. In the Imperial Roman era, Ptolemy used trigonometry to determine the positions of stars in the sky, while Nicomachus and other ancient philosophers revived ancient number theory and harmonics. In Late antiquity, Pappus of Alexandria wrote his Collection, summarizing the work of his predecessors, while Diophantus' Arithmetica dealt with the solution of arithmetic problems by way of pre-modern algebra. Later authors such as Theon of Alexandria, his daughter Hypatia, and Eutocius of Ascalon wrote commentaries on the authors making up the ancient Greek mathematical corpus.

The works of ancient Greek mathematicians were copied in the medieval Byzantine period and translated into Arabic and Latin, where they exerted influence on mathematics in the Islamic world and in Medieval Europe. During the Renaissance, the texts of Euclid, Archimedes, Apollonius, and Pappus in particular went on to influence the development of early modern mathematics. Some problems in Ancient Greek mathematics were solved only in the modern era by mathematicians such as Gauss, and attempts to prove or disprove Euclid's parallel line postulate spurred the development of non-Euclidean geometry.

Etymology

Greek mathēmatikē (Ancient Greek: μαθηματική) derives from the Ancient Greek: μάθημα, romanized: máthēma, Attic Greek: [má.tʰɛː.ma] Koinē Greek: [ˈma.θi.ma], from the verb manthano, "I learn". Strictly speaking, a máthēma could be any branch of learning, or anything learnt; however, since antiquity certain mathēmata were granted special status: arithmetic, geometry, astronomy, and harmonics. These four mathēmata, which appear listed together around the time of Archytas and Plato, would later become the medieval quadrivium.

Origins

Pythagoras with a tablet of ratios, detail from The School of Athens by Raphael (1509). Modern historians question whether Pythagoras made any mathematical discoveries such as the Pythagorean theorem.

The origins of Greek mathematics are not well documented. The earliest known written treatises on Ancient Greek mathematics, starting with Hippocrates of Chios in the 5th century BC, have been lost, and the early history of mathematics must be reconstructed from information passed down through later authors, beginning in the mid-4th century BC. Much of the knowledge about Ancient Greek mathematics in this period is thanks to references by Plato, Aristotle, and from quotations of Eudemus of Rhodes' histories of geometry and arithmetic by later authors. These references provide near-contemporary accounts for many mathematicians active in the 4th century BC. Euclid's Elements is also believed to contain many theorems that are attributed to mathematicians in the preceding centuries.

Bronze Age

Main articles: Egyptian mathematics and Babylonian mathematics

The earliest advanced civilizations in Greece were the Minoan and later Mycenaean (1500-1200 BC) civilizations, both of which flourished in the second half of the Bronze Age. While these civilizations possessed writing, and many Linear B documents written in Mycenaean Greek have been deciphered, no mathematical writings have yet been discovered. When Greek writing re-emerge in the 7th century BC after the Bronze Age collapse, it was based on an entirely new system derived from the Phoenician alphabet, with papyrus from Ancient Egyptian being the preferred medium.

Unlike later Greek mathematics, the mathematics from the preceding Babylonian and Egyptian Bronze Age civilizations were primarily focused on land mensuration and accounting; although some mathematical problems went beyond purely utilitarian aims, including constructing artificial scenarios involving the solution of quadratic equations, there are no signs of explicit theoretical concerns. Though no direct evidence of transmission is available, it is generally thought that Babylonian and Egyptian mathematics had an influence on the younger Greek culture, possibly through an oral tradition of mathematical problems over the course of centuries.

Archaic period

Later traditions attribute the origin of Greek mathematics to either Thales of Miletus, one of the legendary Seven Sages of Greece, or to Pythagoras of Samos, both of whom are said to have visited Egypt and Babylon and learned mathematics there. However, modern scholarship tends to be skeptical of such claims as neither Thales or Pythagoras left any writings behind that were available in the Classical period. Additionally, widespread literacy and the scribal culture that would have supported the transmission of mathematical treatises did not emerge fully until the 5th century; the oral literature of their time was primarily focused on public speeches and recitations of poetry. The standard view among historians is that the discoveries Thales and Pythagoras are credited with, such as Thales' Theorem, the Pythagorean theorem, and the Platonic solids, are the product of attributions by much later authors.

Classical Greece

One of the earliest documented results in Ancient Greek mathematics is the Lune of Hippocrates, from the late 5th century BC. The shaded portion in the upper left is the same area as the shaded part of the triangle

The earliest traces of Greek mathematical treatises appear in the second half of the fifth century BC. According to Eudemus, Hippocrates of Chios was the first to write a book of Elements in the tradition later continued by Euclid. Fragments from another treatise written by Hippocrates on lunes also survives, possibly as an attempt to square the circle. Eudemus' states that Hippocrates studied with an astronomer named Oenopides of Chios. Other mathematicians associated with Chios include Andron and Zenodotus, who may be associated with a "school of Oenopides" mentioned by Proclus.

Although many stories of the early Pythagoreans are likely apocryphal, including stories about people being drowned or exiled for sharing mathematical discoveries, some fifth-century Pythagoreans may have contributed to mathematics. Beginning with Philolaus of Croton, a contemporary of Socrates, studies in arithmetic, geometry, astronomy, and harmonics became increasingly associated with Pythagoreanism. Fragments of Philolaus' work are preserved in quotations from later authors. Aristotle is one of the earliest authors to associate Pythagoreanism with mathematics, though he never attributed anything specifically to Pythagoras.

Mathematical discussions from other fifth-century philosophers are also extant: Antiphon claimed to be able to construct a rectilinear figure with the same area as a given circle, while Hippias is credited with a method for squaring a circle with a neusis construction. Protagoras and Democritus debated the possibility for a line to intersect a circle at a single point. According to Archimedes, Democritus also asserted, apparently without proof, that the area of a cone was 1/3 the area of a cylinder with the same base, a result which was later proved by Eudoxus of Cnidus.

Mathematics in the time of Plato

Archytas, a Pythagorean philosopher and friend of Plato, is credited with important early discoveries in geometry and harmonics.

While Plato was not a mathematician himself, numerous early mathematicians, including Archytas, Theaetetus, and Eudoxus, were associated with Plato or with his Academy, and Plato mentions mathematics in several of his dialogues, including the Meno, the Theaetetus, the Republic, and the Timaeus.

Archytas, a Pythagorean philosopher from Tarentum, was a friend of Plato who made several mathematical discoveries. Archytas is often credited with books VII to IX in the Elements, which deal with the Euclidean algorithm, prime numbers, mean ratios, and perfect numbers. Archytas solved the problem of doubling the cube, now known to be impossible with only a compass and a straightedge, with an alternative method, systematized the Pythagorean means, and made contributions to optics and mechanics.

Theaetetus, who figures as a character in the Platonic dialogue named after him, where he is working on a problem given to him by Theodorus of Cyrene to demonstrate that the square roots of several numbers from 3 to 17 are irrational, a construction now known as the Spiral of Theodorus. Theaetetus is traditionally credited with much of the work contained in Books X of Euclid's Elements, concerned with incommensurable magnitudes, Book XIII, which outlines the construction of the regular polyhedra. Although some of the regular polyhedra were certainly known prior to Theaetetus, he is credited with the systematic construction of them, and the proof that only five of them exist.

Another mathematician associated with Plato's academy is Eudoxus of Cnidus, developed a theory of proportion in book V of the Elements. Archimedes also credits Eudoxus of Cnidus with two propositions in book XII of Euclid's Elements, proving that the volume of a cone is one-third the volume of a cylinder with the same base, which use an early form of calculus known as the method of exhaustion. This method is also used by Archimedes himself in order to find an approximation to π (Measurement of the Circle) and to prove that the area enclosed by a parabola and a straight line is 4/3 times the area of a triangle with equal base and height (Quadrature of the Parabola). Eudoxus also developed an astronomical calendar, now lost, that remains partially preserved by an imitation in poetic form called Phaenomena by Aratus. Eudoxus seems to have founded a school of mathematics in Cyzicus, where one of Eudoxus' students, Menaechmus went on to develop a theory of conic sections.

Hellenistic and early Roman period

Ancient Greek mathematics reached its acme during the Hellenistic era and early Roman periods following Alexander the Great's conquest of the Eastern Mediterranean, Egypt, Mesopotamia, the Iranian plateau, Central Asia, and parts of India, leading to the spread of the Greek language and culture across these regions. Koine Greek became the lingua franca of scholarship throughout the Hellenistic world, and the mathematics of the Classical period merged with Egyptian and Babylonian mathematics to give rise to Hellenistic mathematics, and several centers of learning appeared during the Hellenistic period, of which the most important one was the Musaeum in Alexandria, in Ptolemaic Egypt.

Although few in number, Hellenistic mathematicians actively communicated with each other via letters; who were then responsible for distributing publication consisted of passing and copying someone's work among colleagues. Working at the Library of Alexandria, Euclid collected many previous mathematical results and theorems in the Elements, a compilation of many of the works of his predecessors that would become a canon of geometry and elementary number theory for many centuries. Archimedes, building on the work in Elements, used the method of exhaustion to approximate Pi (Measurement of a Circle), measured the surface area and volume of a sphere (On the Sphere and Cylinder), devised a mechanical method for developing solutions to mathematical problems using the law of the lever, (Method of Mechanical Theorems), and a developed method for representing very large numbers in order to show that the number of grains of sand filling the universe was not uncountable.(The Sand-Reckoner), Apollonius of Perga, in his extant work Conics, refined and developed the theory of conic sections first outlined by Menaechmus, Euclid, and Conon of Samos. Trigonometry was developed around the time of Hipparchus, an early astronomer, and both trigonometry and astronomy further developed by Ptolemy in his Almagest.

Construction problems

Main article: Straightedge and compass construction

Much of the extant literature on hellenistic mathematics deals with three construction problems: Doubling the Cube, Angle trisection, and Squaring the circle, all of which are now known to be impossible with only a straight edge and a compass, however, many attempts were made using neusis constructions including the Cissoid of Diocles, Quadratrix, and the Conchoid of Nicomedes.

The construction of the Platonic solids, outlined in Book XIII of Euclid's elements, is often credited to Theaetetus, a mathematician who worked in Plato's academy.

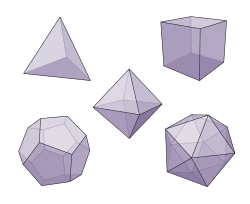
The constructions regular polygons and polyhedra had already been known by the time of the publication of Euclid's elements. Archimedes extended this in a now lost work by constructing the semiregular polyhedra, also sometimes known as Archimedean solids. A work transmitted as "Book XIV" of Euclid's Elements, likely written a few centuries later by Hypsicles, provides a historical development after Theatetus; Aristaeus the Elder's comparison of five figures and Apollonius of Perga's Comparison of the Dodecahedron and the Icosahedron. Another book, transmitted as "Book XV" of Euclid's elements, which was compiled in the 6th century CE, provides further developments.

Many of the works on the solution of construction problems became part of a standard curriculum of works which were studied during the Hellenistic period: Data and Porisms by Euclid, several works by Apollonius of Perga including Cutting off a ratio, Cutting off an area, Determinate section, Tangencies, and Neusis, and several works dealing with loci, including Plane Loci and Conics by Apollonius, Solid Loci by Aristaeus the Elder, Loci on a Surface by Euclid, and On Means by Eratosthenes of Cyrene. All of these works other than Data, Conics Books I to VII, and Cutting off a ratio are lost. However, a rough outline of the contents of can be obtained in Book 7 of the Collection of Pappus of Alexandria, who provides brief epitomes of each of the works, along with lemmas for Cutting off an area, Determinate section, Tangencies, Porisms, Neusis, Plane Loci, and Book VIII of the Conics.

The study of optics in Ancient Greece was also considered a part of geometry. An extant work on Catoptrics is dubiously attributed to Euclid, Archimedes is known to have written a now lost work on catoptrics, and another work, On Burning Mirrors, by Diocles is extant in an arabic translation.

Astronomy

The Little Astronomy, a collection of shorter works from the 4th–2nd century BC, mostly with astronomical relevance, have survived because they were bundled together as an astronomy curriculum beginning in the 2nd century AD and transmitted as a group: Theodosius's Spherics, Autolycus's On the Moving Sphere, Euclid's Optics and Phaenomena, Theodosius's On Habitations and On Days and Nights, Aristarchus's On the Sizes and Distances, Autolycus's On Risings and Settings, and Hypsicles's On Ascensions. These works are all extant in Vaticanus gr. 204, which also contains Apollonius's Conics books I-IV and the commentary by Eutocius, and Euclid's Catoptrics and his Data with an introduction by Marinus of Neapolis. This collection was translated into Arabic with a few additions such as Euclid's Data, Menelaus's Spherics (which only survives in Arabic), and various works by Archimedes as the Middle Books, intermediate between Euclid's Elements and Ptolemy's Almagest.

Around the 2nd century BC, the works of Babylonian astronomers became available to Ancient Greek mathematicians. The development of trigonometry as a synthesis of Babylonian and Greek methods in mathematical astronomy is commonly attributed to Hipparchus, who made extensive astronomical observations and wrote several mathematical treatises; however, all of Hipparchus's works have been lost with the exception of his Commentary on the Phaenomena of Eudoxus and Aratus, a critical commentary on a lost treatise by Eudoxus and a popular poem based on it by Aratus about astronomical phenomena, which was preserved bundled among other commentary on Aratus's poem.

In the 2nd century AD, Claudius Ptolemy compiled the observations of Hipparchus and other astronomers and wrote a work now called the Almagest explaining the motions of the stars and planets according to a geocentric model, and calculated out chord tables to a higher degree of precision than had been done previously, along with an instruction manual, Handy Tables.

Arithmetic

Building on the works of the earlier Pythagoreans, Nicomachus of Gerasa wrote an Introduction to Arithmetic which would go on to receive later commentary in Neopythagoreanism. The continuing influence of Platonism in mathematics is shown by another extant work, Mathematics Useful For Understanding Plato, by Theon of Smyrna, written around the same time. Diophantus wrote on polygonal numbers and a work in pre-modern algebra (Arithmetica),

Applied mathematics

Much of the work represented by authors such as Euclid, Archimedes, Apollonius, Hipparchus, and Diophantus was of a very advanced level and rarely mastered outside a small circle. Ancient Greek mathematics was not limited to theoretical works but was also used in other activities, such as business transactions and in land mensuration, as evidenced by extant texts where computational procedures and practical considerations took more of a central role. Examples of applied mathematics around this time include the construction of analogue computers like the Antikythera mechanism, the accurate measurement of the circumference of the Earth by Eratosthenes, and the mathematical and mechanical works of Heron.

Mathematics in late antiquity

The mathematicians in the later Roman era from the 4th century onward generally had few notable original works, however, they are distinguished for their commentaries and expositions on the works of earlier mathematicians. These commentaries have preserved valuable extracts from works which have perished, or historical allusions which, in the absence of original documents, are precious because of their rarity.

Pappus' Collection

Pappus of Alexandria compiled a canon of results of earlier mathematics in the Collection in eight books, of which part of book II and books III through VII are extant in Greek and book VIII is extant in Arabic. The collection attempts to sum up the whole of Ancient Greek mathematics up to that time as interpreted by Pappus: Book III is framed as a letter to Pandrosion, a mathematican in Athens, and discusses three construction problems and attempts to solve them: Doubling the Cube, Angle trisection, and Squaring the Circle. Book IV discusses classical geometry, which Pappus divides into plane geometry, Line geometry, and Solid geometry, and includes a discussion of Archimedes' construction of the Arbelos, otherwise only known via a Pseudo-archimedean work, Book of Lemmas. Book V discusses isoperimetric figures, summarizing otherwise lost works by Zenodotus and Archimedes on isoperimetric plane figures and solid figures, respectively. Book VI deals with astronomy, providing commentary on some of the works of the Little Astronomy corpus. Book VII deals with analysis, providing epitomes and lemmas from otherwise lost works. Book VIII deals with mechanics. The Greek version breaks off in the middle of a sentence discussing Hero of Alexandria, but a complete edition of the book survives in Arabic.

Commentaries

The commentary tradition, which had begun during the Hellenistic period, continued into late antiquity. The first known commentary on the Elements was written by Hero of Alexandria, who likely set the format for future commentaries. Serenus of Antinoöpolis wrote a lost commentary on the Conics of Apollonius, along with two works that survive, Section of a Cylinder and Section of a Cone, expanding on specific subjects in the Conics. Pappus wrote a commentary on Book X of the elements, dealing with incommensurable magnitudes. Heliodorus of Larissa wrote a summary of the Optics.

Many of the late antique commentators were associated with Neoplatonist philosophy; Porphyry of Tyre, a student of Plotinus, the founder of Neoplatonism, wrote a commentary on Ptolemy's Harmonics. Iamblichus, who was himself a student of Porphyry, wrote a commentary on Nicomachus' Introduction to Arithmetic. In Alexandria in the 4th century, Theon of Alexandria wrote commentaries on the writings of Ptolemy, including a commentary on the Almagest and two commentaries on the Handy Tables, one of which is more of an instruction manual ("Little Commentary"), and another with a much more detailed exposition and derivations ("Great Commentary"). Hypatia, Theon's daughter, also wrote a commentary on Diophantus' Arithmetica and a commentary on the Conics of Apollonius, which have not survived.

In the 5th century, in Athens, Proclus wrote a commentary on Euclid's elements, which the first book survives. Proclus' contemporary, Domninus of Larissa, wrote a summary of Nicomachus' Introduction to Arithmetic, while Marinus of Neapolis, Proclus' successor, wrote an Introduction to Euclid's Data. Meanwhile in Alexandria, Ammonius Hermiae, John Philoponus and Simplicius of Cilicia wrote commentaries on the works of Aristotle that preserve information on earlier mathematicians and philosophers. Eutocius of Ascalon,(c. 480–540 AD) another student of Ammonius, wrote commentaries that are extant on Apollonius' Conics along with some treatises of Archimedes: On the Sphere and Cylinder, Measurement of a Circle, and On Balancing Planes (though the authorship of the last one is disputed). In Rome, Boethius, seeking to preserve Ancient Greek philosophical, translated works on the quadrivium into Latin, deriving much of his work on Arithmetic and Harmonics from Nicomachus.

After the closure of the Neoplatonic schools by the emperor Justinian in 529 AD, the institution of mathematics as a formal enterprise entered a decline. However, two mathematicians connected to the Neoplatonic tradition were commissioned to build the Hagia Sophia: Anthemius of Tralles and Isidore of Miletus. Anthemius constructed many advanced mechanisms and wrote a work On Surprising Mechanisms which treats "burning mirrors" and skeptically attempts to explain the function of Archimedes' heat ray. Isidore, who continued the project of the Hagia Sophia after Anthemius' death, also supervised the revision of Eutocius' commentaries of Archimedes. From someone in Isidore's circle we also have a work on polyhedra that is transmitted pseudepigraphically as Book XV of Euclid's Elements.

Reception and legacy

A papyrus fragment (P. Oxy. 29) from Euclid's Elements Book II, dated to approximately 100 AD.

The majority of mathematical treatises written in Ancient Greek, along with the discoveries made within them, have been lost; around 30% of the works known from references to them are extant. Authors whose works survive in Greek manuscripts include: Euclid, Autolycus of Pitane, Archimedes, Aristarchus of Samos, Philo of Byzantium, Biton of Pergamon, Apollonius of Perga, Hipparchus, Theodosius of Bithynia, Hypsicles, Athenaeus Mechanicus, Geminus, Hero of Alexandria, Apollodorus of Damascus, Theon of Smyrna, Cleomedes, Nicomachus, Ptolemy, Cleonides, Gaudentius, Anatolius of Laodicea, Aristides Quintilian, Porphyry, Diophantus, Alypius, Heliodorus of Larissa, Pappus of Alexandria, Serenus of Antinoöpolis, Theon of Alexandria, Proclus, Marinus of Neapolis, Domninus of Larissa, Anthemius of Tralles, and Eutocius.

The earliest surviving papyrus to record a Greek mathematical text is P. Hib. i 27, which contains a parapegma of Eudoxus' astronomical calendar, along with several ostraca from the 3rd century BC that deal with propositions XIII.10 and XIII.16 of Euclid's Elements. A papyrus recovered from Herculaneum contains an essay by the Epicurean philosopher Demetrius Lacon on Euclid's Elements.

Most of the oldest extant manuscripts for each text date from the 9th century onward, copies of works written during and before the Hellenistic period. The two major sources of manuscripts are Byzantine-era codices, copied some 500 to 1500 years after their originals, and Arabic translations of Greek works; what has survived reflects the preferences of readers in late antiquity along with the interests of mathematicians in the Byzantine empire and the medieval Islamic world who preserved and copied them.

Despite the lack of original manuscripts, the dates for some Greek mathematicians are more certain than the dates of surviving Babylonian or Egyptian sources because a number of overlapping chronologies exist, though many dates remain uncertain.

Byzantine mathematics

With the closure of the Neoplatonist schools in the 6th century, Greek mathematics declined in the medieval Byzantine period, although many works were preserved in medieval manuscript transmission and translated into first Syriac and Arabic, and later into Latin. The transition to miniscule manuscript in the 9th century, however, many works that were not copied during this time period were lost, although a few uncial manuscripts do survive. Many surviving works are derived from only a single manuscript; such as Pappus' Collection and Books I-IV of the Conics. Many of the surviving manuscripts originate from two scholars in this period in the circle of Photios I, Leo the Mathematician and Arethas of Caesarea. Scholia written in the margins of Euclid's elements that have been copied throughout multiple extant manuscripts that were also written by Arethas, derived from Proclus' commentary along with many commentaries on Euclid which are now lost. The works of Archimedes survived in three different recensions in manuscripts from the 9th and 10th centuries; two of which are now lost after being copied, the third of which, the Archimedes Palimpsest, was only rediscovered in 1906.

In the later Byzantine period, George Pachymeres wrote a summary of the quadrivium, and Maximus Planudes wrote scholia on the first two books of Diophantus.

Medieval Islamic mathematics

Numerous mathematical treatises were translated into Arabic in the 9th century; many works that are only extent today in Arabic translation, and there is evidence for several more that have since been lost.

Medieval Islamic scientists such as Alhazen developed the ideas of the Ancient Greek geometry into advanced theories in optics and astronomy, and Diophantus' Arithmetica was synthezied with the works of Al-Khwarizmi and works from Indian mathematics to develop a theory of algebra.

The following works are extant only in Arabic translations:

• Apollonius, Conics books V to VII, Cutting Off of a Ratio
• Archimedes, Book of Lemmas
• Diocles, On Burning Mirrors
• Diophantus, Arithmetica books IV to VII
• Euclid, On Divisions of Figures, On Weights
• Menelaus, Sphaerica
• Hero, Catoptrica, Mechanica
• Pappus, Commentary on Euclid's Elements book X, Collection Book VIII
• Ptolemy, Planisphaerium,

Additionally, the work Optics by Ptolemy only survives in a Latin translations of the Arabic translation of a Greek original.

In Latin Medieval Europe

Cover of Diophantus' Arithmetica in Latin

The works derived from Ancient Greek mathematical writings that had been written in late antiquity by Boethius and Martianus Capella had formed the basis of early medieval quadrivium of arithmetic, geometry, astronomy, and music. In the 12th century the original works of Ancient Greek mathematics were translated into Latin first from Arabic by Gerard of Cremona, and then from the original Greek a century later by William of Moerbeke.

Renaissance

The publication of Greek mathematical works increased their audience; Pappus's collection was published in 1588, Diophantus in 1621. Diophantus would go on to influence Pierre de Fermat's work on number theory; Fermat scribbled his famous note about Fermat's Last theorem in his copy of Arithmetica. Descartes, working through the Problem of Apollonius from his edition of Pappus, proved what is now called Descartes' theorem and laid the foundations for Analytic geometry.

Modern mathematics

Ancient Greek mathematics constitutes an important period in the history of mathematics: fundamental in respect of geometry and for the idea of formal proof. Greek mathematicians also contributed to number theory, mathematical astronomy, combinatorics, mathematical physics, and, at times, approached ideas close to the integral calculus.

Richard Dedekind acknowledged Eudoxus's theory of proportion as an inspiration for the Dedekind cut, a method of contructing the real numbers.

See also

• Timeline of ancient Greek mathematicians
• List of Greek mathematicians
• Music of ancient Greece – Musical traditions of ancient Greece

References

• Acerbi, Fabio (2018), "Hellenistic Mathematics", in Keyser, Paul T; Scarborough, John (eds.), Oxford Handbook of Science and Medicine in the Classical World, pp. 268–292, doi:10.1093/oxfordhb/9780199734146.013.69, ISBN 978-0-19-973414-6, retrieved 2021-05-26
• Boyer, Carl B. (1991), A History of Mathematics (3rd ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8
• Cameron, A. (1990), "Isidore of Miletus and Hypatia: On the Editing of Mathematical Texts", Greek, Roman, and Byzantine Studies, 31 (1): 103–127
• Fowler, D. H. (1999), The Mathematics of Plato's Academy (2nd ed.), Clarendon Press
• Høyrup, J. (1990), "Sub-scientific mathematics: Undercurrents and missing links in the mathematical technology of the Hellenistic and Roman world" (PDF) (Unpublished manuscript, written for Aufstieg und Niedergang der römischen Welt)
• Knorr, Wilbur R. (1986), The Ancient Tradition of Geometric Problems
• Knorr, Wilbur R. (1996), "The method of indivisibles in Ancient Geometry", Vita Mathematica, MAA Press, pp. 67–86
• Mansfeld, J. (2016), Prolegomena Mathematica: From Apollonius of Perga to the Late Neoplatonism. With an Appendix on Pappus and the History of Platonism, Brill, ISBN 978-90-04-32105-2
• Netz, Reviel (2022), A New History of Greek Mathematics, Cambridge University Press, ISBN 978-1-108-83384-4
• Netz, Reviel (2014), "The problem of Pythagorean mathematics", in Huffman, Carl A. (ed.), A History of Pythagoreanism, Cambridge University Press, pp. 167–184, doi:10.1017/CBO9781139028172.009, ISBN 978-1-107-01439-8
• Schofield, Malcolm (2014), "Archytas", in Huffman, Carl A. (ed.), A History of Pythagoreanism, Cambridge University Press, pp. 69–87, doi:10.1017/CBO9781139028172.009, ISBN 978-1-107-01439-8

Further reading

• A. Barker, Porphyry’s Commentary on Ptolemy’s Harmonics
• A. Barker, Greek Musical Writings, Vol. 2: Harmonic and Acoustic Theory
• A. Bernard, “Ancient Rhetoric and Greek Mathematics: A Response to a Modern Historiographical Dilemma,”
• I. Bodnár, Oenopides of Chius: A Survey of the Modern Literature with a Collection of the Ancient Testimonia
• Burton, David M. (1997), The History of Mathematics: An Introduction (3rd ed.), The McGraw-Hill Companies, Inc., ISBN 978-0-07-009465-9
• M. F. Burnyeat, “Plato on Why Mathematics Is Good for the Soul,” Proceedings of the British Academy 2000
• M. F. Burnyeat, “The Philosophical Sense of Theaetetus’ Mathematics,” 1978
• L. Corry, A Brief History of Number
• S. Cuomo, Pappus of Alexandria and the Mathematics of Late Antiquity
• Christianidis, Jean, ed. (2004), Classics in the History of Greek Mathematics, Dordrecht: Kluwer, ISBN 978-1-4020-0081-2
• Cooke, Roger (1997), The History of Mathematics: A Brief Course, Wiley-Interscience, ISBN 978-0-471-18082-1
• Derbyshire, John (2006), Unknown Quantity: A Real And Imaginary History of Algebra, Joseph Henry Press, ISBN 978-0-309-09657-7
• E. J. Dijksterhuis, Archimedes
• M. N. Fried, and S. Unguru, Apollonius of Perga’s Conica: Text, Context, Subtext
• Heath, Thomas Little (1981) [First published 1921], A History of Greek Mathematics, Dover publications, ISBN 978-0-486-24073-2
• Heath, Thomas Little (2003) [First published 1931], A Manual of Greek Mathematics, Dover publications, ISBN 978-0-486-43231-1
• Huffman, Archytas
• Huffman, Philolaus
• A. Jones, A Portable Cosmos
• R. W. Knorr, The Evolution of the Euclidean Elements, 1975
• H. Mendell, “Reflections on Eudoxus, Callippus and Their Curves: Hippopedes and Callippopedes,”
• I. Mueller, Philosophy of Mathematics and Deductive Structure in Euclid’s Elements
• Netz, “Eudemus of Rhodes, Hippocrates of Chios and the Earliest Form of a Greek Mathematical Text,”
• R. Netz, Ludic Proof: Greek Mathematics and the Alexandrian Aesthetics
• R. Netz, The Shaping of Deduction in Greek Mathematics
• O. Pedersen, A Survey of the Almagest: With Annotation and New Commentary by Alexander Jones
• D. N. Sedley, “Epicurus and the Mathematicians of Cyzicus,”
• M. Sialaros, J. Christianidis, and A. Megremi (eds.), “On Mathemata: Commenting on Greek and Arabic Mathematical Texts,”
• Sing, Robert; Berkel, Tazuko Angela van; Osborne, Robin (2022), Numbers and numeracy in the Greek polis, Brill, ISBN 978-90-04-46721-7
• Stillwell, John (2004), Mathematics and its History (2nd ed.), Springer Science + Business Media Inc., ISBN 978-0-387-95336-6
• Szabó, Árpád; Szabó, Árpád (1978), The Beginnings of Greek Mathematics, Budapest: Akadémiai Kiadó, ISBN 978-963-05-1416-3
• S. Unguru, “On the Need to Rewrite the History of Greek Mathematics,” Archive for History of Exact Sciences 15 (1975): 67-114
• G. Vlastos, “Elenchus and Mathematics: A Turning-Point in Plato’s Philosophical Development,”
• I. Yavetz, “On the Homocentric Spheres of Eudoxus,” Archive for History of Exact Sciences

External links

• Vatican Exhibit
• History of Mathematics
• MacTutor archive of History of Mathematics