From Wikipedia, the free encyclopedia
This user page is being considered for deletion in accordance with Wikipedia's deletion policy .
Please discuss the matter at this page's entry Miscellany for deletion page.
You are welcome to edit this page, but please do not blank, merge, or move it, or remove this notice, while the discussion is in progress. For more information, see the Guide to deletion .%5B%5BWikipedia%3AMiscellany+for+deletion%2FUser%3ADVdm%5D%5D MFD
This...
This user has been on Wikipedia for 20 years, 1 month and 23 days .
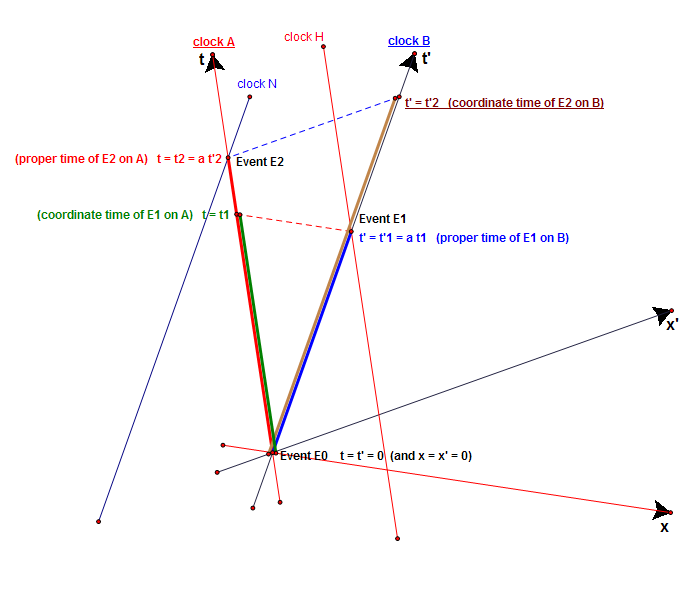
On page 230 in this appendix to "Science At the Crossroads" , Dingle writes:
(start quote)
Thus, between events E0 and E1, A advances by
t
1
{\displaystyle \color {ForestGreen}{t_{1}}}
t
1
′
=
a
t
1
{\displaystyle \color {Blue}{t'_{1}=at_{1}}}
rate of A
rate of B
=
t
1
a
t
1
=
1
a
>
1
(3)
{\displaystyle {\frac {\color {ForestGreen}{\text{rate of A}}}{\color {Blue}{\text{rate of B}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{at_{1}}}}={\frac {1}{a}}>1\qquad {\text{(3)}}}
...
Thus, between events E0 and E2, B advances by
t
2
′
{\displaystyle \color {Brown}{t'_{2}}}
t
2
=
a
t
2
′
{\displaystyle \color {Red}{t_{2}=at'_{2}}}
rate of A
rate of B
=
a
t
2
′
t
2
′
=
a
<
1
(4)
{\displaystyle {\frac {\color {Red}{\text{rate of A}}}{\color {Brown}{\text{rate of B}}}}={\frac {\color {Red}{at'_{2}}}{\color {Brown}{t'_{2}}}}=a<1\qquad {\text{(4)}}}
Equations (3) and (4) are contradictory: hence the theory requiring them must be false.
(end quote) Dingle should have written as follows:
(start correction)
Thus, between events E0 and E1, A, which is not present at both events, advances by
t
1
{\displaystyle \color {ForestGreen}{t_{1}}}
present at both events, by
t
1
′
=
a
t
1
{\displaystyle \color {Blue}{t'_{1}=at_{1}}}
rate of clock not present at both events E0 and E1
rate of clock present at both events E0 and E1
=
coordinate time of E1
proper time of E1
=
rate of A
rate of B
=
t
1
t
1
′
=
t
1
a
t
1
=
1
a
>
1
(3)
{\displaystyle {\frac {\color {ForestGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color {Blue}{\text{rate of clock present at both events E0 and E1}}}}={\frac {\color {ForestGreen}{\text{coordinate time of E1}}}{\color {Blue}{\text{proper time of E1}}}}={\frac {\color {ForestGreen}{\text{rate of A}}}{\color {Blue}{\text{rate of B}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{t'_{1}}}}={\frac {\color {ForestGreen}{t_{1}}}{\color {Blue}{at_{1}}}}={\frac {1}{a}}>1\qquad {\text{(3)}}}
...
Thus, between events E0 and E2, B, which is not present at both events, advances by
t
2
′
{\displaystyle \color {Brown}{t'_{2}}}
present at both events, by
t
2
=
a
t
2
′
{\displaystyle \color {Red}{t_{2}=at'_{2}}}
rate of clock not present at both events E0 and E2
rate of clock present at both events E0 and E2
=
coordinate time of E2
proper time of E2
=
rate of B
rate of A
=
t
2
′
t
2
=
t
2
′
a
t
2
′
=
1
a
>
1
(4)
{\displaystyle {\frac {\color {Brown}{\text{rate of clock not present at both events E0 and E2}}}{\color {Red}{\text{rate of clock present at both events E0 and E2}}}}={\frac {\color {Brown}{\text{coordinate time of E2}}}{\color {Red}{\text{proper time of E2}}}}={\frac {\color {Brown}{\text{rate of B}}}{\color {Red}{\text{rate of A}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{t_{2}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{at'_{2}}}}={\frac {1}{a}}>1\qquad {\text{(4)}}}
Equations (3) and (4) are consistent and say that any event's coordinate time is always larger than its proper time: hence there is no reason to say that the theory requiring them must be false.
(end correction) DVdm 12:18, 6 August 2007 (UTC)